http://stanford.edu/~rqi/pointnet2/
Overview
Pointnet achieved high performance in point cloud classification and segmentation tasks by utilizing transformation matrix inference and pooling. However, PointNet was unable to successfully extract local features due to the unordered feature of the point cloud. In order to eliminate these shortcomings, PointNet++ obtained state-of-the-art performance on challenging benchmarks of 3D point clouds at the time by making use of a sampling layer to extract local features, a grouping layer to group features, and PointNet itself.
Features of Poitnet++
Figure 1 shows the PointNet++ architecture.
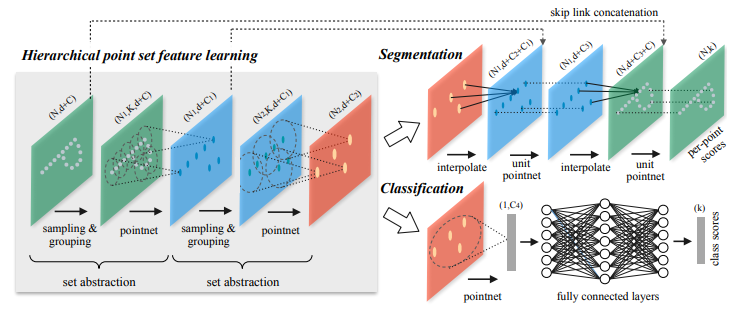
As we can see in figure 1, the feature of PointNet++ is sampling and grouping in the low-level layers.
By going thru these layers, the features of the point cloud are going to be aggregated.
- Sampling layer
The layer is going to sample given input points using iterative farthest point sampling(FPS). It has better coverage of the entire point set given the same number of centroids compared with random sampling.
What is interesting in this layer is, the paper says “In contrast to CNNs that scan the vector space agnostic of data distribution, our sampling strategy generates receptive fields in a data-dependent manner.”
- Groping layer
The input to this layer is N x (d + C), N is the number of points, d is the dimension of coordinates and C is the number of features. The grouping layer associates a group of points close to the centroid with the centroid by using kNN or Ball query. The shape of each exported group from this layer is N x K x (d + C). The K is the number of points around these centroids, but K is not fixed.
- PointNet layer
The PointNet is applied for those groups from the previous layer.
Reference
[1]Charles R. Qi, Li Yi, Hao Su, Leonidas J. Guibas Stanford University “PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space”