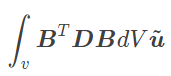Finite Element Method for Stress Analysis

Followed the equations from the page below. Thanks for greate explanations.

Basically, I wrote up this flow, but slightly changed something since it is wrong sometimes.

https://qiita.com/Altaka4128/items/41101c96729b68d7c96f

The formulation of the finite element method for stress analysis

The FEM formulation is as follows.

\displaystyle \boldsymbol{K}\boldsymbol{\tilde{U}} = \boldsymbol{F} \\ \boldsymbol{K} = \sum_e \boldsymbol{K}_e \\ \begin{aligned} &\boldsymbol{K} : \text{Stiffness Matrix} \\ &\boldsymbol{\tilde{U}} : \text{Nodal Displacement Vector} \\ &\boldsymbol{F} : \text{Nodal Force Vector}\\ &\boldsymbol{K}_e : \text{Element Stiffness Matrix} \end{aligned}

Displacement and Stiffness Matrix

Relation of Stress and Strain

\left\{ \begin{array}{ll} \epsilon_x = \frac{1}{E}(\sigma_x - \nu (\sigma_y + \sigma_z)) \\ \epsilon_y = \frac{1}{E}(\sigma_y - \nu (\sigma_x + \sigma_z)) \\ \epsilon_z = \frac{1}{E}(\sigma_z - \nu (\sigma_x + \sigma_y)) \\ \gamma_{xy} = \frac{2(1+\nu)}{E}\tau_{xy} \\ \gamma_{yz} = \frac{2(1+\nu)}{E}\tau_{yz} \\ \gamma_{xz} = \frac{2(1+\nu)}{E}\tau_{xz} \end{array} \right. \\ \begin{aligned} &\sigma : Vertical Stress \\ &\tau : Shear Stress \\ &\epsilon : Vertical Strain \\ &\gamma : Engineering Shear Strain \\ &E : Young's Modulus \\ &\nu : Poisson's Ratio \end{aligned}\\ \boldsymbol{\sigma} = \boldsymbol{D} \boldsymbol{\epsilon} \\ \boldsymbol{\sigma} = \begin{bmatrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{yz} \\ \tau_{xz} \\ \tau_{xy} \end{bmatrix}, \boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{bmatrix} \\ \boldsymbol{D} = \frac{E}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1-\nu && \nu && \nu && 0 && 0 && 0 \\ \nu && 1-\nu && \nu && 0 && 0 && 0 \\ \nu && \nu && 1-\nu && 0 && 0 && 0 \\ 0 && 0 && 0 && \frac{1-2\nu}{2} && 0 && 0 \\ 0 && 0 && 0 && 0 && \frac{1-2\nu}{2} && 0 \\ 0 && 0 && 0 && 0 && 0 && \frac{1-2\nu}{2} \end{bmatrix}

By the way, In the case of two-dimensional analysis, formulas are used differently for plane stress and plane strain.

Relationship between strain and displacement

\boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{bmatrix} = \begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial w}{\partial z} \\ \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \\ \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \end{bmatrix} \\ \begin{aligned} &u : Displacement-in-the-x-direction \\ &v : Displacement-in-the-y-direction \\ &w : Displacement-in-the-z-direction \\ \end{aligned}

Tetrahedral first-order element

Using the shape functions, strain can be represented by the nodal displacements and the B-matrix.

This is shown for the case of a tetrahedral first-order element.

\left\{ \begin{array}{ll} u = N_1 u_1 + N_2 u_2 + N_3 u_3 + N_4 u_4 \\ v = N_1 v_1 + N_2 v_2 + N_3 v_3 + N_4 v_4 \\ w = N_1 w_1 + N_2 w_2 + N_3 w_3 + N_4 w_4 \end{array} \right. \\ \begin{aligned} &u_i : Displacement\space in\space the\space x-direction\space at\space node\space i \\ &v_i : Displacement\space in\space the\space y-direction\space at\space node\space i \\ &w_i : Displacement\space in\space the\space z-direction\space at\space node\space i \\ &N_i : Shape\space Function \end{aligned} \\ \left\{ \begin{array}{ll} N_1 = 1-a-b-c \\ N_2 = a \\ N_3 = b \\ N_4 = c \end{array} \right.

Tetrahedral second-order element

Here is the normalized coordinate transformation formula for the tetrahedral second-order element

\begin{align*} &\text{Nodes of the isoparametric coordinates:} \\ &1. \quad (\xi = 0, \eta = 0, \zeta = 0) \\ &2. \quad (\xi = 1, \eta = 0, \zeta = 0) \\ &3. \quad (\xi = 0, \eta = 1, \zeta = 0) \\ &4. \quad (\xi = 0, \eta = 0, \zeta = 1) \\ &5. \quad (\xi = 0.5, \eta = 0.5, \zeta = 0) \\ &6. \quad (\xi = 0.5, \eta = 0, \zeta = 0.5) \\ &7. \quad (\xi = 0, \eta = 0.5, \zeta = 0.5) \\ &8. \quad (\xi = 0, \eta = 0.5, \zeta = 0) \\ &9. \quad (\xi = 0.5, \eta = 0, \zeta = 0) \\ &10. \quad (\xi = 0, \eta = 0, \zeta = 0.5) \\ \\ &\text{Shape functions:} \\ &N_1 = \xi(2\xi - 1) \\ &N_2 = \eta(2\eta - 1) \\ &N_3 = \zeta(2\zeta - 1) \\ &N_4 = (1-\xi-\eta-\zeta)(2(1-\xi-\eta-\zeta)-1) \\ &N_5 = 4\xi\eta \\ &N_6 = 4\xi\zeta \\ &N_7 = 4\eta\zeta \\ &N_8 = 4\eta(1-\xi-\eta-\zeta) \\ &N_9 = 4\xi(1-\xi-\eta-\zeta) \\ &N_{10} = 4\zeta(1-\xi-\eta-\zeta) \\ \end{align*}

The differentiation of displacement is represented by differentiation of shape funtions.

\frac{\partial u}{\partial x} = \frac{\partial N_1}{\partial x}u_1 + \frac{\partial N_2}{\partial x}u_2 + \frac{\partial N_3}{\partial x}u_3 + \frac{\partial N_4}{\partial x}u_4

So, strain is represented by displacement and B matrix.

\boldsymbol{\epsilon} = \boldsymbol{B} \tilde{\boldsymbol{u}} \\ \tilde{\boldsymbol{u}} = \begin{bmatrix} u_1 \\ v_1 \\ w_1 \\ u_2 \\ v_2 \\ w_2 \\ u_3 \\ v_3 \\ w_3 \\ u_4 \\ v_4 \\ w_4 \end{bmatrix} \\ \boldsymbol{B} = \begin{bmatrix} \frac{\partial N_1}{\partial x} && 0 && 0 && \frac{\partial N_2}{\partial x} && 0 && 0 && \frac{\partial N_3}{\partial x} && 0 && 0 && \frac{\partial N_4}{\partial x} && 0 && 0 \\ 0 && \frac{\partial N_1}{\partial y} && 0 && 0 && \frac{\partial N_2}{\partial y} && 0 && 0 && \frac{\partial N_3}{\partial y} && 0 && 0 && \frac{\partial N_4}{\partial y} && 0 \\ 0 && 0 && \frac{\partial N_1}{\partial z} && 0 && 0 && \frac{\partial N_2}{\partial z} && 0 && 0 && \frac{\partial N_3}{\partial z} && 0 && 0 && \frac{\partial N_4}{\partial z} \\ 0 && \frac{\partial N_1}{\partial z} && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial z} && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial z} && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial z} && \frac{\partial N_4}{\partial y} \\ \frac{\partial N_1}{\partial z} && 0 && \frac{\partial N_1}{\partial x} && \frac{\partial N_2}{\partial z} && 0 && \frac{\partial N_2}{\partial x} && \frac{\partial N_3}{\partial z} && 0 && \frac{\partial N_3}{\partial x} && \frac{\partial N_4}{\partial z} && 0 && \frac{\partial N_4}{\partial x} \\ \frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x} && 0 \end{bmatrix}

To determine the B matrix(the differentiation of shape matrix), the Jacobian matrix is required.

\boldsymbol{J}= \begin{bmatrix} \frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} && \frac{\partial z}{\partial a} \\ \frac{\partial x}{\partial b} && \frac{\partial y}{\partial b} && \frac{\partial z}{\partial b} \\ \frac{\partial x}{\partial c} && \frac{\partial y}{\partial c} && \frac{\partial z}{\partial c} \end{bmatrix} \\ \begin{aligned} &\frac{\partial x}{\partial a} = \sum_{i=1}^4 \frac{\partial N_i}{\partial a}x_i & \frac{\partial x}{\partial b} = \sum_{i=1}^4 \frac{\partial N_i}{\partial b}x_i & \frac{\partial x}{\partial c} = \sum_{i=1}^4 \frac{\partial N_i}{\partial c}x_i \\ &\frac{\partial y}{\partial a} = \sum_{i=1}^4 \frac{\partial N_i}{\partial a}y_i & \frac{\partial y}{\partial b} = \sum_{i=1}^4 \frac{\partial N_i}{\partial b}y_i & \frac{\partial y}{\partial c} = \sum_{i=1}^4 \frac{\partial N_i}{\partial c}y_i \\ &\frac{\partial z}{\partial a} = \sum_{i=1}^4 \frac{\partial N_i}{\partial a}z_i & \frac{\partial z}{\partial b} = \sum_{i=1}^4 \frac{\partial N_i}{\partial b}z_i & \frac{\partial z}{\partial c} = \sum_{i=1}^4 \frac{\partial N_i}{\partial c}z_i \\ \end{aligned}

\begin{bmatrix} \frac{\partial N_i}{\partial a} \\ \frac{\partial N_i}{\partial b} \\ \frac{\partial N_i}{\partial c} \end{bmatrix} = \boldsymbol{J} \begin{bmatrix} \frac{\partial N_i}{\partial x} \\ \frac{\partial N_i}{\partial y} \\ \frac{\partial N_i}{\partial z} \end{bmatrix} \\

\begin{bmatrix} \frac{\partial N_i}{\partial x} \\ \frac{\partial N_i}{\partial y} \\ \frac{\partial N_i}{\partial z} \end{bmatrix} = \boldsymbol{J}^{-1} \begin{bmatrix} \frac{\partial N_i}{\partial a} \\ \frac{\partial N_i}{\partial b} \\ \frac{\partial N_i}{\partial c} \end{bmatrix}

Here, the displacement and strain within the elements can be expressed as follows

{ \boldsymbol{u} = \boldsymbol{N} \tilde{\boldsymbol{u}} \\ }

\boldsymbol{\epsilon} = \boldsymbol{B} \tilde{\boldsymbol{u}} \\ \boldsymbol{N} = \begin{bmatrix} N_1 && 0 && N_2 && 0 && N_3 && 0 && N_4 && 0 \\ 0 && N_1 && 0 && N_2 && 0 && N_3 && 0 && N_4 \\ \end{bmatrix}\\

Let’s consider virtual work equation below

{ \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV \tilde{\boldsymbol{u}} = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS }

\boldsymbol{K_e} \tilde{\boldsymbol{u}} = \boldsymbol{f_e} \\ \boldsymbol{K_e} = \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV \\ \boldsymbol{f_e} = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\ \boldsymbol{K_e} : Element\space Stiffness\space Matrix\\ \boldsymbol{f_e} : Equivalent\space nodal\space force

When the above equation is substituted into the virtual work equation, the element stiffness matrix is obtained

\begin{equation} \boldsymbol{K_e} = \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} \, dV \end{equation}

We will transform to a normal coordinate system

\begin{align} \boldsymbol{K_e} &= \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} \, dV \\ &= \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} |\boldsymbol{J}| \, da \, db \, dc \\ &= w \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} |\boldsymbol{J}| \end{align} \\ w = \frac{1}{6} \text{: weight coefficient}

Body Forces

Body forces act throughout the volume of an object. They don’t result from any direct physical contact with another body, but rather are forces that act on the object due to external factors. A classic example of a body force is gravitational force. Every part of an object, down to its individual molecules, experiences the pull of gravity, no matter where the object is located or what other objects are around it. Another example of a body force is electromagnetic force in the case of charged bodies.

\begin{align} \int_v \boldsymbol{N}^T \boldsymbol{b} dV &= \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} \boldsymbol{N}^T \boldsymbol{b} |\boldsymbol{J}| \\ &= w \boldsymbol{N}^T \boldsymbol{b} |\boldsymbol{J}| \\ \end{align} \\ w = \frac{1}{6}: weight\space coefficient

In the case of gravity, it becomes the density multiply by acceleration vector.

Surface Forces

Surface forces, on the other hand, act on the external surface of a body. They arise due to direct contact with another object or medium. Surface forces can be further categorized based on how they act. For example, a normal force is a surface force that acts perpendicular to the surface, like the force a table exerts upward on a book resting on it. Tension and friction are also examples of surface forces. Another type of surface force is pressure, which acts normal to the surface, but is distributed over the area of the surface.

Stiffness Matrix

In the case of 3 dimensions, the global stiffness matrix can be represented as follows, given N nodal points.

\boldsymbol{K_e} = \begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1, 3N} \\ K_{21} & K_{22} & \cdots & K_{2, 3N} \\ \vdots & \vdots & \ddots & \vdots \\ K_{3N, 1} & K_{3N, 2} & \cdots & K_{3N, 3N} \end{bmatrix}

For a tetrahedral element, since there are 4 nodal points, the element stiffness matrix is a 12×12 matrix. Therefore, to add element stiffness matrex to the global stiffness matrix, it’s necessary to determine the corresponding positions in the matrix. If the nodal numbers of the triangular elements are denoted by i, j, k, and l, the positions to store in the global stiffness matrix can be represented as follows.