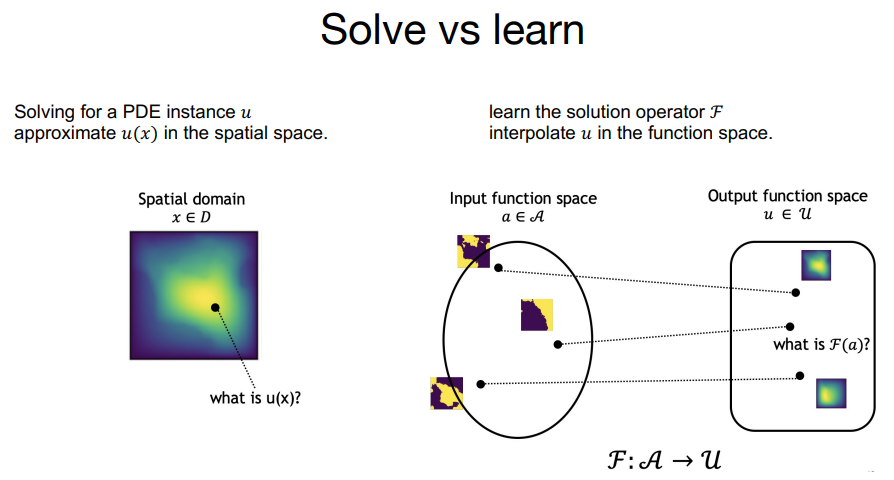
What this field is going to do
The previously introduced Physics Informed Neural Network (PINN) directly estimates the solution (field) of PDEs by introducing a loss related to the partial differential equations. While it was a very interesting attempt, it focused on solving only for a single condition, which limited its versatility. Additionally, poor convergence was observed in some cases.
Recently, various new approaches have been undertaken, which I would like to introduce. These involve learning about partial differential equations using neural operators. This means, rather than learning about a specific partial differential equation, the effort is to learn the solutions of parametric partial differential equations. What does this mean? It means trying to solve the problem of converting from one general function to another by learning from a large number of equations for which the answers are known (or the data can be measured).
Fourier Neural Operator, and its Training Example
In reality, while various deep learning models have been proposed, Zongyi Li has reported on the convolutional network model shown in the following diagram, which applies spectral decomposition.
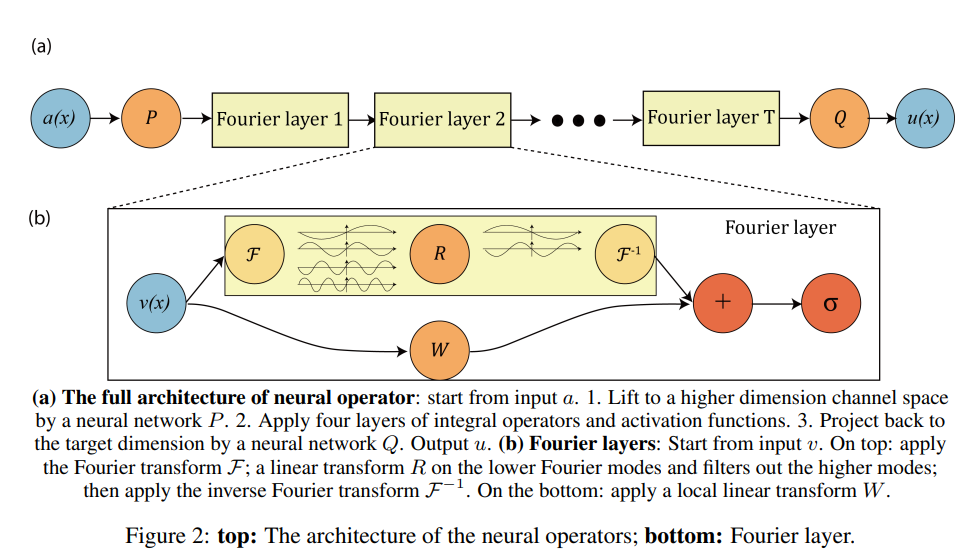
https://arxiv.org/abs/2010.08895
The structure is very simple, where the output of function A, which determines a specific partial differential equation and takes input from the spatial domain, becomes the solution U of the PDE. Notably, due to being a convolutional network, the data structure should be a simple grid structure. If we ignore the reasons why this is a good choice, what their process looks straightforward.
I will present an interesting slide that the authors have created to understand the concept visually.
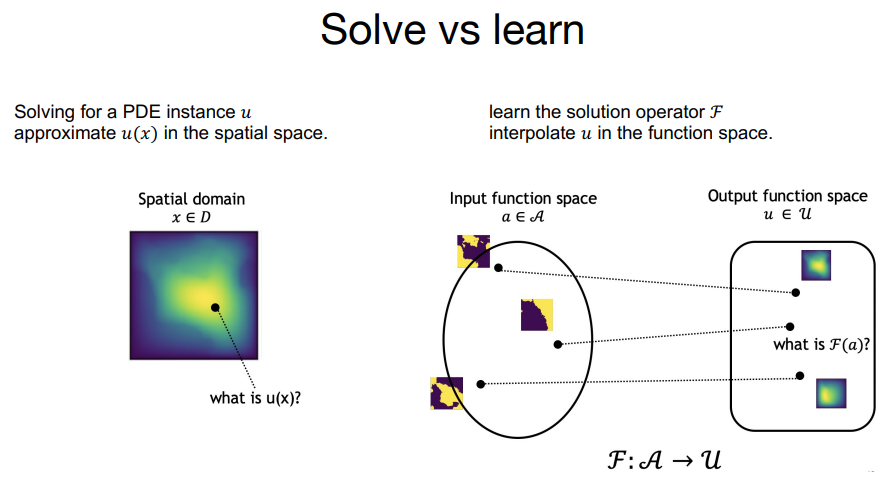
https://zongyi-li.github.io/neural-operator/Neural-Operator-CS159-0503-2022.pdf
If we disregard the structure of the neural network, the task being performed is quite simple. As for the specific problems they solved 4 examples
Experiments
They solved below 4 problems
- Burgers Equation
- Darcy Flow
- Navier-Stokes Equation
- Bayesian Inverse Problem
Let’s focus on the relatively simpler to explain topic among them: 2. Darcy Flow.
They consider the steady-state of the 2-d Darcy Flow equation on the unit box which is the second
order, linear, elliptic PDE.
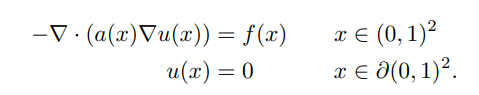
In this context, once the function ( a ) is determined, a specific partial differential equation is defined. The authors attempt to create a universal solver by randomly generating the function ( a ), obtaining its solutions, and using them for learning.
But why do they do such a thing?
What is the advantage of doing this?
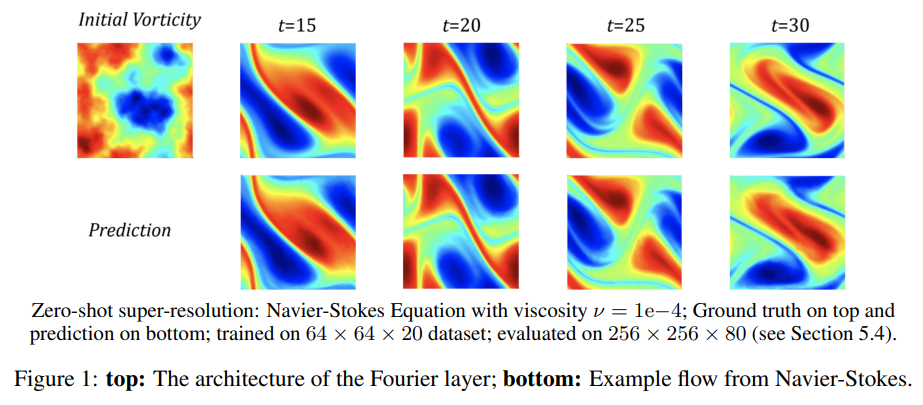
One reason could be the significantly fast computation speed. This is likely due to the efficiency of parallel processing in convolutional operations. If a universal PDE solver could be learned, even though the learning process might be time-consuming, it could potentially provide rapid, high-quality solutions for specific PDEs afterwards. Additionally, the authors present an intriguing concept: Zero-shot super-resolution.
Zero-shot super-resolution
It seems that models trained at low resolution can be effectively applied to high-resolution problems. The following is a figure quoted from the paper, showing an example using the Navier-Stokes equation.
Next to read and to understand
What I am interested in, and next to read is here.
https://www.jmlr.org/papers/volume24/21-1524/21-1524.pdf
https://arxiv.org/pdf/2111.03794.pdf
I’m still not fully understanding it, but I became interested after seeing the following slide. It’s about the Physics-informed neural operator. From what I can gather from the figure, it seems that after performing the learning of the neural operator as a preprocessing step, the intention is to solve specific problems using PINN (Physics Informed Neural Network). I anticipate that this approach will enable handling problems with complex boundary conditions that were difficult to control using PINN.