About
I am paying attention to this technology because there are increasing opportunities to manipulate and utilize features, namely embedding vectors. For example, embeddings have been widely used in language models for some time, and they are also commonly used in the world of vision and in multimodal approaches. Furthermore, with the development of foundational models, few-shot learning is becoming more convenient. Additionally, there is the retrieval of such information, namely vector databases. In this way, it can be said that our opportunities to manipulate embeddings are increasing.
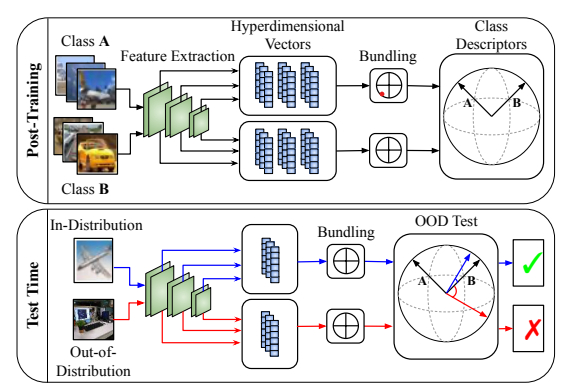
While very high-dimensional feature vectors are difficult to handle due to factors such as the curse of dimensionality, hyperdimensional vectors exhibit interesting results in out-of-distribution detection tasks due to some of their properties.
To clarify and introduce some key points, the paper below defines three specific properties that enable the execution of Out-of-Distribution (OOD) detection tasks using Hyperdimensional Vectors.
Hyperdimensional Feature Fusion for Out-Of-Distribution Detection
Hyperdimensional Computing
By defining the following three properties, we are able to perform Out-of-Distribution (OOD) detection tasks using Hyperdimensional Vectors.
Bundling (a.k.a. superposition)
The bundling ⊕ operation is used to store a representation of multiple input vectors that retains similarity to all of the input vectors. Even if you add several vectors into a vector, it preserves all of features.
It means that under the condision that given random vectors a, b and c, the vector a
a \oplus b \approx a \oplus c \approx a \oplus b \oplus c
(a \oplus b) \oplus c \approx a \oplus (b \oplus c)
Binding
The binding ⊗ operation is used to combine a set of vectors into one representation that is dissimilar to all of the input vectors. The binding operation will generate a vector orthogonal to all of the input vectors in the cosine similarity space.
\text{sim}(a, b) \approx \text{sim}(a \otimes c, b \otimes c)Encoding
To get feature vector in hyper dimensional space, projecting operation is appliced for original feature vector. By this projcecting, a hyper dimensional vector has traits below list.
- High Dimensionality: Hyperdimensional vectors, by virtue of their high dimensionality, can represent a vast amount of data points with high precision. This property allows for the distinction between in-distribution and out-of-distribution data by providing a rich, high-dimensional space where in-distribution data can cluster tightly while out-of-distribution samples are more likely to fall outside these clusters.
- Orthogonality: In a high-dimensional space, random vectors are almost always orthogonal to each other. This property can be exploited for OOD detection by ensuring that representations of in-distribution data are orthogonal to those of potential out-of-distribution data. This makes it easier to identify when new inputs significantly deviate from the expected distribution.
- Similarity Metrics: Hyperdimensional computing often uses similarity metrics (e.g., cosine similarity, Hamming distance) to quantify the closeness of vectors. For OOD detection, these metrics can help determine how far an incoming data point deviates from the known distributions. A significant deviation in terms of similarity could flag a data point as being out-of-distribution.