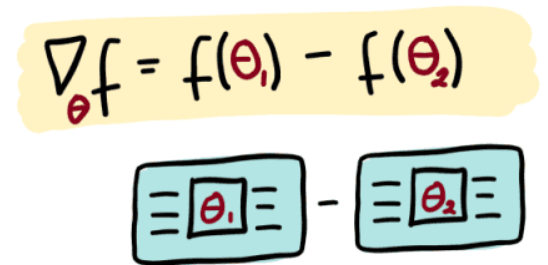
About
Special Unitary Group of degree (n)
SU(n) refers to the n-dimensional case of the special unitary group, which plays an important role in mathematics and physics, especially quantum mechanics(for example SU(2)), The elements of this group are unitary matrices that undergo linear transformations in a two-dimensional complex vector space and have determinant 1.
Definition
Conditions to be satisfied
The following 2 conditions satisfy when it is SU(2).
\begin{align}
U^\dagger U = U U^\dagger = I \\
\det(U) = 1
\end{align}Representation
The general form of SU(2) matrix is represented as following using Pauli matrices.
U = e^{i (\alpha \sigma_x + \beta \sigma_y + \gamma \sigma_z)}where a, b, and c are real values. It means that there are 3 independent parameters in SU(2). Incidentally, this represents a gate that rotates a quantum state around an arbitrary axis on the Bloch sphere. Let’s say we have a rotation gate that rotate quantum state along with arbitrary axis-n. The rotation gate R is written as following
\begin{align}
R_n(\theta)=e^{-i\frac{\theta}{2} \vec{n} \cdot \vec{\sigma}}=e^{-i\theta (n_x \sigma_x + n_y \sigma_y + n_z \sigma_z)/2}
\end{align}these 3 Pauli matrices are written as
\begin{align}
\sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\\
\sigma_y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}\\
\sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
\end{align}And Pauli matrices have following characteristic,
\begin{align}
\sigma_x^2=\sigma_y^2=\sigma_z^2=1\\
\sigma_x \sigma_y= i \sigma_z \\
\sigma_y \sigma_z = i \sigma_x \\
\sigma_z \sigma_x = i \sigma_y \\
\sigma_x \sigma_y = - \sigma_y \sigma_x \\
(\vec{n} \cdot \vec{\sigma})^2=I
\end{align}and (3) is expanded to (13), and (14) by using (13). There is Taylor expansion is behind
\begin{align}
R_n(\theta)=cos\frac{\theta}{2}I-i(\vec{n} \cdot \vec{\sigma})sin\frac{\theta}{2} \\
=cos\frac{\theta}{2}I-isin\frac{\theta}{2}(n_x \sigma_x + n_y \sigma_y + n_z \sigma_z)
\end{align}
This representation shows a method of representing a general element of the SU(2) group through an exponential map, and is related to the rotation of spin-1/2 particles and the manipulation of qubits in quantum mechanics.
An example of expansion
Let’s see expansion of exponential matrix in the cause of sigma 3, pauli Z gate
\begin{align}
\exp(it\sigma_3) = \sum_{n=0}^\infty \frac{(it\sigma_3)^n}{n!}\\
\exp(it\sigma_3) = \left(\sum_{k=0}^\infty \frac{(it)^{2k}}{(2k)!} \right) I + \left(\sum_{k=0}^\infty \frac{(it)^{2k+1}}{(2k+1)!} \right) \sigma_3\\
\exp(it\sigma_3) = \cos(t) I + i\sin(t) \sigma_3\\
\exp(it\sigma_3) = \begin{pmatrix} \cos(t) & 0 \\ 0 & \cos(t) \end{pmatrix} + i\begin{pmatrix} \sin(t) & 0 \\ 0 & -\sin(t) \end{pmatrix}\\
=\begin{pmatrix} \cos(t) + i\sin(t) & 0 \\ 0 & \cos(t) - i\sin(t) \end{pmatrix} = \begin{pmatrix} e^{it} & 0 \\ 0 & e^{-it} \end{pmatrix}
\end{align}Since pauli matrix repeatedly gets to be identity matrix.
\sigma_3^0 = I \\ \sigma_3^1 = \sigma_3 \\ \sigma_3^2 = I \\ \sigma_3^3 = \sigma_3 \\ \sigma_3^4 = I \\
By using Baker-Campbell-Hausdorff formula, we can represent the form as another one
e^{iX} = \cos \|X\| I + i \sin \|X\| \frac{X}{\|X\|}