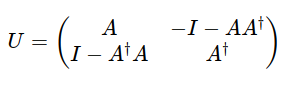Cholesky and QR Decomposition

Cholesky Decomposition

A positive definite Hermite matrix is decompose to lower triangular matrix L and its conjugate transpose matrix L*. It is used for covariance matrix decomposition many times since it can be applied to semi-positive definite matrix.

\Sigma=LL^T

This is special case of LU decomposition that utilizes characteristic of Hermiticity.

Code

import numpy as np

def cholesky_decomposition(A):

    n = A.shape[0]
    L = np.zeros_like(A)
    for i in range(n):
        for j in range(i + 1):
            if i == j:
                L[i, j] = np.sqrt(A[i, i] - np.sum(L[i, :j]**2))
            else:
                L[i, j] = (A[i, j] - np.sum(L[i, :j] * L[j, :j])) / L[j, j]
    
    return L

QR decomposition

QR decomposition is a method to decompose an arbitrary matrix A into an orthogonal matrix Q and an upper triangular matrix R. Specifically, it is expressed as follows:

A=QR

Here, Q is an orthogonal matrix (consisting of vectors whose rows and columns are mutually orthogonal and whose length is 1), R is an upper triangular matrix.
The decomposition is applicable to any matrix (square matrix, rectangular matrix, non-positive definite matrix, etc.), used for solution of linear equations, least squares eigenvalue calculation, principal component analysis

Code

The decomposition is implemented using gram schmidt orthogonalization procedure

import numpy as np

def gram_schmidt_qr(A):

    m, n = A.shape
    Q = np.zeros((m, n))
    R = np.zeros((n, n))
    
    # グラム・シュミットによる正規直交化
    for j in range(n):
        # Aの列ベクトルを取得
        v = A[:, j]
        
        # 既に計算した直交基底に対してプロジェクションを行い、Rの成分を計算
        for i in range(j):
            R[i, j] = np.dot(Q[:, i], v)
            v = v - R[i, j] * Q[:, i]
        
        # Rの対角成分を計算し、それを使って正規化
        R[j, j] = np.linalg.norm(v)
        Q[:, j] = v / R[j, j]

    return Q, R