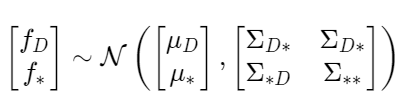About
Pick up a sample from Multi-Variant Gaussian Distribution is sometimes important for applications like Gaussian Process.
Multivariate Gaussian Distribution
As we can see in (1), the Multivariate Gaussian Distribution is represented as mean vector mu, and covariance matrix sigma, And also see in (2), the covariance matrix is decomposed using Cholesky Decomposition because the matrix is positive definite Hermite.
\begin{align}
y \sim \space \N(\mu, \Sigma)\\
\Sigma=LL^T
\end{align}Create a sample from Standard Gaussian Distribution
\begin{align}
x \sim \space \N(0, I)\\
p(y)=p(Lx+\mu) \propto exp((y-\mu)^T\Sigma^{-1} (y-\mu))
\end{align}