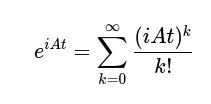The difference
\begin{align}
det(SU(N))=1\\
det(U(N))=e^{i\theta}
\end{align}The effect to Quantum Bit
It causes global phase on qubit
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle \\
\to U|\psi\rangle = e^{i\theta}(\alpha'|0\rangle + \beta'|1\rangle)The representation using Hermite
As we can see in my articles (https://eye.kohei-kevin.com/2024/06/27/why-unitary-is-represented-using-hermite/, https://eye.kohei-kevin.com/2024/06/20/pure-state-representation-using-density-matrix/), U(2) and SU(2)
\begin{align}
U(2) = e^{i (\delta I+\alpha \sigma_x + \beta \sigma_y + \gamma \sigma_z)}\\
SU(2) = e^{i (\alpha \sigma_x + \beta \sigma_y + \gamma \sigma_z)}
\end{align}In the case of U(2), Hermite H can take any Hermite matrix, but in the case of SU(2), Hermite H should have traceless basis. Because of this restriction, The generator of SU(2) should be traceless, and The H should be linear combination of Pauli matrices.