About
Understanding EHVI is quite complicated. So by following the BoTorch code and some papers, I will quickly see the usage and basic concept,
https://arxiv.org/abs/2105.08195
Bayesian Estimation based on Expected Hyper Volume Improvement(EHVI)
in BoTorch Tutorial (https://botorch.org/tutorials/multi_objective_bo), what they do is to call 3 functions, fit_gpytorch_mll, qNoisyExpectedHypervolumeImprovement and optimize_acqf.
The fit_gpytorch_mll simply optimizes model parameters based on marginal likelihood loss (training), and the qNoisyExpectedHypervolumeImprovement defines what kind of acquisition function to use as metrics. And then, optimize_acqf gives us candidates in explanatory variables space where we could increase hyper volume improvement.
But what is Hypervolume itself or its process to be computed?
Code in Tutorial
def optimize_qnehvi_and_get_observation(
model, train_x, train_obj, sampler
):
"""Optimizes the qEHVI acquisition function, and returns a new candidate and observation."""
# partition non-dominated space into disjoint rectangles
acq_func = qNoisyExpectedHypervolumeImprovement(
model=model,
ref_point=problem.ref_point.tolist(), # use known reference point
X_baseline=normalize(train_x, problem.bounds),
prune_baseline=True, # prune baseline points that have estimated zero probability of being Pareto optimal
sampler=sampler,
)
# optimize
candidates, _ = optimize_acqf(
acq_function=acq_func,
bounds=standard_bounds,
q=BATCH_SIZE,
num_restarts=NUM_RESTARTS,
raw_samples=RAW_SAMPLES, # used for intialization heuristic
options={"batch_limit": 5, "maxiter": 200},
sequential=True,
)
# observe new values
new_x = unnormalize(candidates.detach(), bounds=problem.bounds)
return new_x
qnehvi_sampler = SobolQMCNormalSampler(sample_shape=torch.Size([MC_SAMPLES]))
fit_gpytorch_mll(mll_qnehvi)
new_x = optimize_qnehvi_and_get_observation(
model_qnehvi, train_x_qnehvi, train_obj_qnehvi, qnehvi_sampler
)
new_obj_true = problem(new_x)
new_obj = new_obj_true + torch.randn_like(new_obj_true) * NOISE_SE
Hypervolume Improvement
The definition of Hypervolume improvement in formula is like this.
\text{HVI}(P_0|P, r) = HV(P ∪ P0|r) − HV(P|r)Suppose we have reference point on the left lower in the graph, and somehow we would like to get pareto front by maximizing 2 objectives. The blue area where is surrounded by pareto front and reference point is so called Hypervolume.
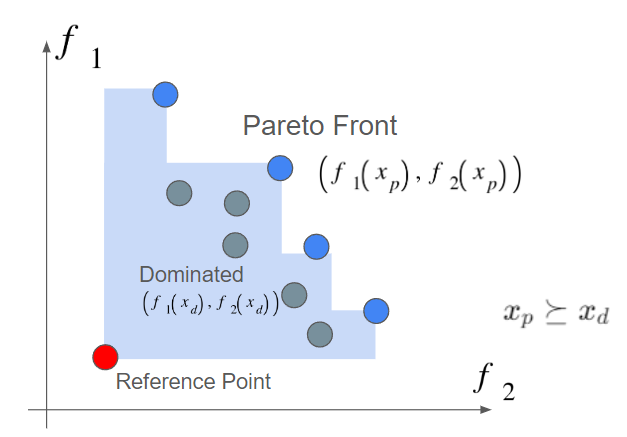
The points xd which are inside the hypervolume is said that these are weakly “dominated” against pareto front.
x_p \succeq x_d
The problem setting we have is to maximize that area by using Gaussian Process for black-box approximation. And the Gaussian Process is regarded as stochastic model, turn out that the hypervolume is also stochastic. So somehow, we would like to get expectation of hypervolume.
Expected Hypervolume Improvement
As we looked at previous section, the idea is to take expectation over Hypervolume based on Gaussian Process. But the problem is, we cannot compute the expectation analytically since it is Hypervolume. So, what the implementation does is to do Monte Carlo (MC) sampling and to take integration over the sampled data. What the SobolQMCNormalSampler in code plays is the role.
\alpha_{\text{EHVI}}(x) = \int \alpha_{\text{EHVI}}(x \mid \mathcal{P}_n) p(f \mid \mathcal{D}_n) \, df\\
\hat{\alpha}_{ \text{NEHVI}}(x) = \frac{1}{N} \sum_{t=1}^{N} \text{HVI}\left(\tilde{f}_t(x) \mid \mathcal{P}_t\right)Optimize Acquisition Function
Once you’ve decided which acquisition function to use, the process will optimize the acquisition function you’ve set. This involves sampling based on the raw samples, calculating metrics like EHV, and optimizing the samples using backpropagation. By taking expectation over samples, you would know EHVI and the next candidate points where it is good to sample.