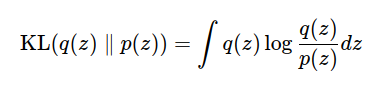About
https://arxiv.org/abs/1206.7051
The main goal is to perform Bayesian inference efficiently and scalable for large data sets and complex Bayesian models. Specifically, it aims to appropriately estimate model parameters and latent variables while reducing the overall computational load by approximating expected values using a subset of data and performing stochastic optimization. This makes it possible to perform Bayesian inference in a realistic amount of time, and it has come to be used in a wide range of application fields.
It is one of the powerful methods for efficiently solving integration problems and recalculation problems in Bayesian inference. It is inefficient to recalculate the entire data set every time new data comes in. SVI solves this problem, and it is important that it can perform Bayesian inference in a scalable manner even on large datasets.
Features summary
- Mini-batch approximation
- Instead of processing the entire data, calculations are performed on a subset of the data, reducing the amount of computation.
- Stochastic optimization
- Calculates approximate gradients based on mini-batches and gradually updates parameters using stochastic gradient descent.
- Variational inference
- An easy-to-handle approximate distribution is introduced instead of the posterior distribution, and inference is performed by minimizing the KL divergence
- Separation of global and local variables
- Global variables that apply to all data and local variables that differ for each data are processed separately, improving efficiency
- Natural gradient method
- Performs efficient optimization in parameter space by taking geometric structure into account.
Basically, the idea is to use Evidence Lower Bound to approximate distribution
\mathcal{L}_{\text{SVI}}(\lambda) \approx \frac{N}{|D_{\text{mini}}|} \sum_{i \in D_{\text{mini}}} \mathbb{E}_{q(\theta; \lambda)}\left[\log p(x_i, \theta)\right] - \mathbb{E}_{q(\theta; \lambda)}\left[\log q(\theta; \lambda)\right]