Sparse Axis Aligned Subspace Bayesian Optimization

About

Bayesian optimization using Gaussian processes is an extremely powerful tool. However, it is well-known that performance can degrade significantly as the input dimensionality increases. This is due to the “curse of dimensionality,” where it becomes difficult to differentiate meaningful information. To address these issues, numerous methods have been proposed. For example,

1. Trust Region method (TuRBO)
2. Variable Selection
3. Embedding
4. Additive Kernel
5. Vanilla Bayesian Optimization

However, I believe there is no definitive conclusion on which method is the best. There have been many reports of good results using TuRBO, but TuRBO is fundamentally an algorithm for single-objective optimization. While a multi-objective version has been proposed, it has not been widely reported yet. Likely, each algorithm has its advantages and disadvantages, and the appropriate choice depends on the specific problem. In this article, I will introduce a method called SAABO(Sparse Axis Aligned Subspace Bayesian Optimization https://arxiv.org/abs/2103.00349), which can be interpreted as a model with 2. variable selection approach.

Formulation

As we can see the paper, some prior probabilities are assumed on the length and variance parameters in kernel function as follows

\begin{align}
\sigma_k^2 \sim LN(0, 10^2)\\
\tau \sim \text{HC}(\alpha)\\
\rho_i \sim \text{HC}(\tau) \quad \text{for } i = 1, \ldots, D\\
f \sim \mathcal{N}(0, K_{\psi_{XX}}) \quad \text{with } \psi = \{\rho_{1:d}, \sigma_k^2\}\\
y \sim \mathcal{N}(f, \sigma^2 I_N)
\end{align}

Here, LN is a Log-Normal distribution, and HC is the Half-Cauchy distribution.

You can see the explanation of both distribution in detail here https://eye.kohei-kevin.com/2024/09/25/log-normal-and-half-cauchy-distribution/, anyway, the distributions are written as

\begin{align}
LN(\mu, \sigma) = LN(x | \mu, \sigma) = \frac{1}{x\sigma\sqrt{2\pi}} e^{-\frac{(\ln x - \mu)^2}{2\sigma^2}} \quad \text{for } x > 0\\
HC(x | \gamma) = \frac{2}{\pi} \frac{\gamma}{x^2 + \gamma^2}
\end{align}

And this model is represented as following graphical model.

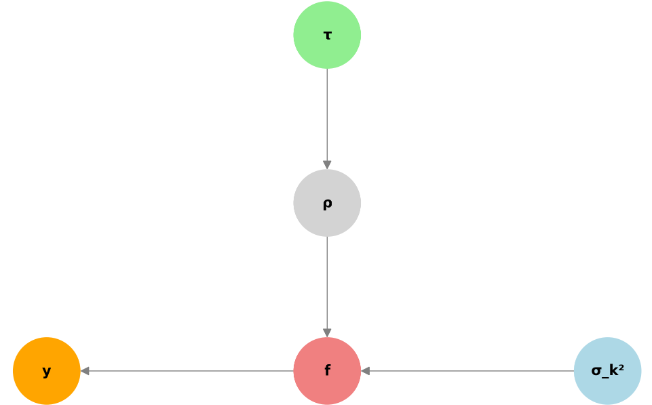
There are 3 properties (priors) that they tried to incorporate into this formulations.

They claimed that

1. The prior on the kernel variance \sigma_k^2 is weak (i.e. non-informative)
2. The level of global shrinkage (i.e. sparsity) is controlled by the scalar \tau \gt 0, which tends to concentrate near zero due to the Half-Cauchy prior.
3. The (inverse squared) length scales \rho_i are also governed by Half-Cauchy priors, and thus they too tend to concentrate near zero.

Optimization

The paper proposes two methods. The first is based on the No-U-Turn Sampler (NUTS) [Hoffman and Gelman, 2014], which is an adaptive variant of Hamiltonian Monte Carlo. The second method is Maximum A Posteriori (MAP) estimation, which sacrifices the accuracy of the posterior approximation for faster runtime.

What we need to care of

The SAABO is an effective method for solving high-dimensional problems and has achieved good performance in many benchmarks. However, it should be noted that it does not scale with the number of data points, and its computational load and memory O(N^3)is the same as vanilla BO. Additionally, optimization using Monte Carlo methods may also take time.

Reference

[1] David Eriksson, Martin Jankowiak “High-Dimensional Bayesian Optimization with Sparse Axis-Aligned Subspaces”, https://arxiv.org/abs/2103.00349

[2] Matthew D Hoffman and Andrew Gelman. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. https://jmlr.org/papers/volume15/hoffman14a/hoffman14a.pdf

[3] C. Hvarfner, E. O. Hellsten, L. Nardi, Vanilla Bayesian Optimization Performs Great in High Dimensions. In International Conference on Machine Learning, 2024.