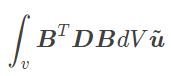Unified form of elastic mechanic

About

The following article provides a detailed summary of the weak form equations in elastic mechanics. However, since it is inconvenient for quick reference, the detailed explanations are omitted here, and only the flow is presented.

Finite Element Method for Stress Analysis

Elastic Mechanic

Balance (Govern) Equation (strong form)

To introduce weak form, strong form is start. It represents balance of force

\begin{align} \nabla\cdot\sigma(u) + \mathbf f &= 0 \quad &&\text{in }\Omega,\\ \end{align}

\begin{aligned} u &= g \quad &&\text{on }\Gamma_D,\\ \sigma(u)\,n &= t \quad &&\text{on }\Gamma_N. \end{aligned}

where $\sigma$ is stress tensor that represents the distribution of internal forces acting on various planes within a continuum.

\sigma = \begin{pmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{pmatrix}

Therefore, the divergence of the stress tensor, $\nabla\cdot\sigma = div \sigma$ , represents the net internal force per unit volume acting at a point within a continuum.

To introduce weak form, a test function 𝑣, which is corresponding to the unknown variable 𝑢, is prepared. Take any test function $v\in [H^1(\Omega)]^d$ with $v=0$ on $\Gamma_D$ . The 𝑣 is multiplied to the strong form, we got this form by performing the domain integral:

\int_\Omega \big(\nabla\cdot\sigma(u)\big)\cdot v\,dx + \int_\Omega \mathbf f\cdot v\,dx = 0.

Apply Gauss’ divergence theorem (integration by parts)

Use the tensor–vector identity (componentwise product rule):

\big(\nabla\cdot\sigma\big)\cdot v \;=\; \nabla\cdot(\sigma v)\;-\;\sigma:\nabla v.

Integrate and invoke the divergence theorem:

\int_\Omega \big(\nabla\cdot\sigma\big)\cdot v\,dx = \int_\Gamma (\sigma n)\cdot v\,ds - \int_\Omega \sigma:\nabla v\,dx.\\ \int_\Gamma (\sigma n)\cdot v\,ds - \int_\Omega \sigma:\nabla v\,dx + \int_\Omega \mathbf f\cdot v\,dx = 0\\ -\int_\Omega \sigma:\nabla v\,dx + \int_{\Gamma_N} t\cdot v\,ds + \int_\Omega \mathbf f\cdot v\,dx = 0

\int_\Omega \sigma(u):\nabla v\,dx = \int_\Omega \mathbf f\cdot v\,dx + \int_{\Gamma_N} t\cdot v\,ds.

Weak Form

By doing partial integral, we get weak form

\begin{align} \int_\Omega \nabla v : \sigma(u) \, d\Omega\\ \int_\Omega \epsilon(v) : \sigma(u) \, d\Omega = \int_\Omega v \cdot f \, d\Omega + \int_{\Gamma_N} v \cdot \bar{t} \, d\Gamma \end{align}

The meaning of : sign

suppose if we have 2nd rank tensor A and B. The meaning of : operation is

A : B = \sum_{i,j} A_{ij} B_{ij} = \text{tr}(A^T B)

Displacement and Strain

\begin{align} \varepsilon(u) = \frac{1}{2} \left( \nabla u + (\nabla u)^T \right)\\ \varepsilon_{ij} = \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \end{align}

How to extend weak form to numeric analysis

How can we extent the weak form (3) to finite element. Let’s do just replacing trial function u and test function v.

\int_\Omega \epsilon(v) : \sigma(u) \, d\Omega = \int_\Omega \epsilon(v) : \mathbb{C} \space \epsilon(u) \, d\Omega \\ = \int_\Omega(B v)^{T} (\mathbb{C} Bu) = \Sigma ({ B^{T} \mathbb{C} B})u = Ku

Oh, but wait… why is test function v suddenly disappeared.

Stress and Strain (with Elasticity Matrix)

\sigma(u) = \mathbb{C} : \varepsilon(u)

Trial and Test Function in Finite Element Analysis

The trial and test functions are represented with shape function Ns.

u_h(x) = \sum_j N_j(x) u_j, \quad v_h(x) = N_i(x)

It is easy to understand how the the trial function is represented. But when it comes to test function, v is gone. Why? The reason is that v is represented by just sampling on points in finite element. That is reason why v is not used directly.

The elasticity tensor (C) represents the material properties and describes the relationship between stress (σ) and strain (ε) at a material point.