About
Many people say that quantum computers can perform calculations faster. But what specific calculations become faster? In reality, quantum computers have many constraints, and without understanding their characteristics, they cannot be used effectively. One application that benefits from improved computational efficiency is solving systems of linear equations. This is known as the Harrow-Hassidim-Lloyd(HHL) algorithm.
Overview
The problem to be solved is a system of linear equations as follows.
\left| b \right\rangle \xrightarrow{} \left| A^{-1} b \right\rangleHere, the computational cost of the general inverse matrix operation is , but HHL can solve it in . However, it is important to note that HHL can only be applied when is a sparse matrix. (I don’t fully understand this yet, but it seems to be more about the solution candidates being sparse rather than the matrix itself being sparse.)
The computation process consists of the following steps:
1. Encoding the problem
2. Phase estimation
3. Extracting information using auxiliary qubits
4. Solution extraction through quantum measurement
Encoding the Problem
As matrix A to be imported to quantum circuits should be hermite matrix, a matrix that you are going to use for linear matrix should be converted to it.
A = \begin{pmatrix} O & A \\ A^\dagger & O \end{pmatrix}, \quad b = \begin{pmatrix} b \\ 0 \end{pmatrix}
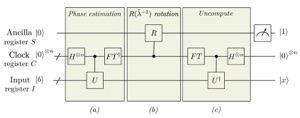
Phase Estimation
Execute the quantum phase estimation algorithm for the unitary operation e^{iA}. Suppose we have the second quantum register, and the eigenvalue of A is read out into the second quantum register.
\left| b \right\rangle \left| 0 \dots 0 \right\rangle_{r-2nd}Note that we can represent quantum state b with eigen vectors u_i.
\left| b \right\rangle = \sum_i \beta_i \left| u_i \right\rangle
By applying QPE to the quantum state, the eigenvalue is read out into the register as it is mentioned like this.
\left| b \right\rangle = \sum_i \beta_i \left| u_i \right\rangle \left| 0 \dots 0 \right\rangle_{r-2nd}
\xrightarrow{\text{QPE}}
\sum_i \beta_i \left| u_i \right\rangle_I \left| \lambda_i \right\rangle_{r-2nd}
Extracting information using ancilla qubits
Add one more ancilla bit and apply a controlled rotation gate that acts on the quantum state as follows.
\left| \lambda \right\rangle_C \left| 0 \right\rangle_S
\rightarrow
\left| \lambda \right\rangle_C
\left( \frac{c}{\lambda} \left| 0 \right\rangle_S + \sqrt{1 - \frac{c^2}{\lambda^2}} \left| 1 \right\rangle_S \right)where c is a normalization constant, determined based on the possible range of eigenvalues.
At this point, note that a simple eigenvalue appears in one of the states. By using this ancilla bit and extracting only the case corresponding to that state, the computation can be performed while reflecting the eigenvalue. The computation for the other ancilla bit state is discarded.
What a smart operation, don’t you think?
Quantum Measurement
My Question…
It’s not a question about HHL itself, but when applying QPE, wouldn’t the eigenvalues corresponding to elements of the original amplitude vector that are zero not be observed? How is this handled? Can someone explain?