Introduction
Topology optimization is a technical field that involves deforming shapes while maximizing physical properties. For example, it is used to design shapes within certain constraints on volume while maintaining structural strength. This time, I tried topology optimization using the density method based on SciPy. While the results aren’t exactly outstanding, it seems to be functioning at a basic, acceptable level for now.
Problem Setting
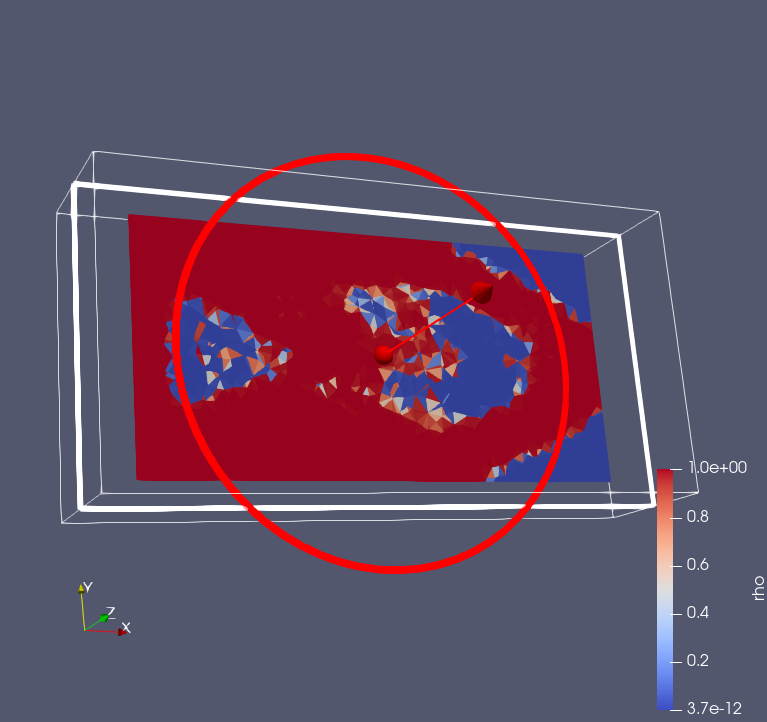
A 3D cubic shape was constructed, with all nodes at x = 0 (Red Region) fully fixed. Then, a force F was applied in the x-direction to the center area of the surface at x = 1 (Green Region). The compliance minimization problem for this setup was solved using topology optimization. I used Tetrahedral Elements, and the total number of elements is 26652.

Solution for the tasks
Data and Shape Structure
Topology optimization can be broadly categorized into two approaches: the density-based method and the level set method.
Each differs in how the shape is represented and updated. The density-based method has relatively low computational cost but often struggles to produce smooth geometries. On the other hand, the level set method directly controls the object’s boundary, making it easier to obtain smooth edges. However, it tends to be more computationally expensive. I will try density-based method in this article.
Optimization Approach
Many optimization methods and technical approaches are suggested in this field. In terms of optimization method,Optimality Criteria (OC) and Method of Moving Asymptotes (MMA) are the most famous approaches.
Objective and Constraints
\begin{aligned}
& \min_{\rho} \quad C(\rho) = \mathbf{u}^T \mathbf{K}(\rho) \mathbf{u} \\
& \text{subject to} \quad \sum \rho_i v_i \leq V^*, \\
& \qquad \quad 0 < \rho_{\min} \leq \rho_i \leq 1
\end{aligned}Formula for Updating
\rho_i^{\text{new}} = \max\left(\rho_{\min}, \min\left(1, \rho_i \cdot \left(-\frac{\partial C / \partial \rho_i}{\lambda} \right)^\eta \right)\right)Here:
- ∂C∂ρi\frac{\partial C}{\partial \rho_i}: Sensitivity of compliance with respect to element ii
- λ: A scaling factor that controls the strength of density update and ensures the volume constraint is satisfied
- η: An exponent usually set to values like 0.5 or 1 (chosen empirically)
This λ is typically adjusted using methods such as the bisection method so that the total updated density does not exceed the prescribed volume constraint.
Bisection Method??
The bisection method is a simple and reliable numerical method for finding the roots (points where =0) of a function. It can be used when the function is monotonic (it only increases or decreases) and you know that there is one solution within the interval.
l1, l2 = 1e-9, 500
while abs(l2 - l1) > tolerance * (l1 + l2) / 2.0:
lmid = 0.5 * (l1 + l2)
scaling_rate = (- dC / (lmid + eps)) ** eta
scaling_rate = np.clip(scaling_rate, 0.5, 1.5)
rho_candidate = np.clip(
rho_e * scaling_rate,
np.maximum(rho_e - move_limit, rho_min),
np.minimum(rho_e + move_limit, rho_max)
)
vol_error = np.mean(rho_candidate_projected) - vol_frac
if vol_error > 0:
l1 = lmid
else:
l2 = lmidEasy to Implement??
It is NOT, actually. Because there are a lot of optimization techniques in the optimization process. Otherwise, it is difficult to stabilize the process. I will add some information in the future in this website
Result
Density in the object
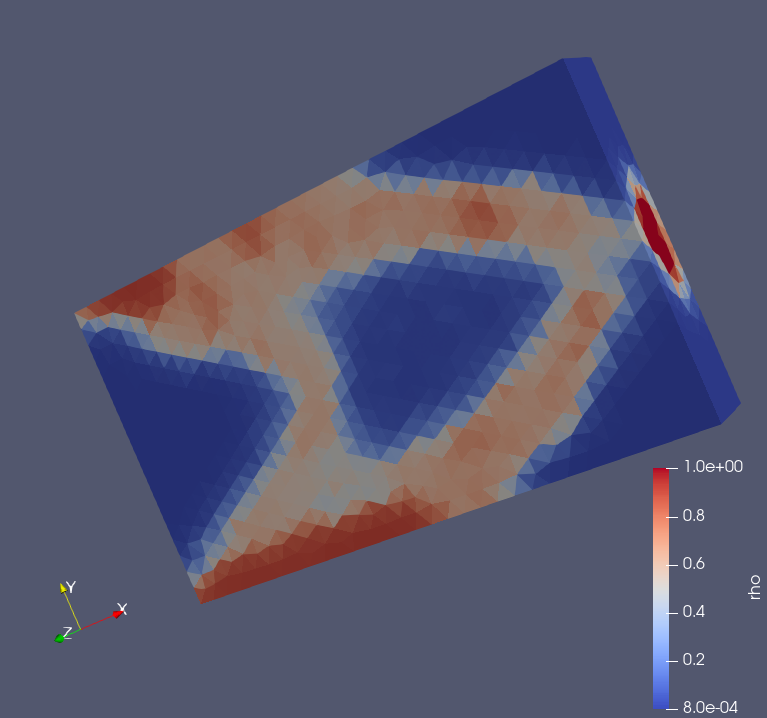
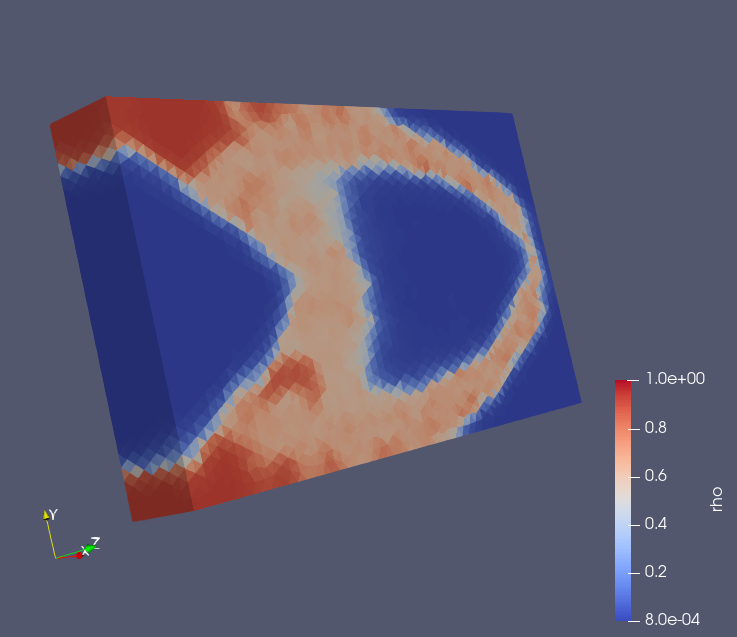
As for the results, they are shown below. This figure illustrates the internal density of the object optimized through topology optimization.
Red indicates regions with high density, while blue represents regions with low density.
When elements on BC are not contained as design elements
When elements on BC are contained as design elements
Parameters for the Experiment
{
"max_iters": 200,
"p": 3.0,
"p_rate": 12.0,
"vol_frac": 0.2,
"vol_frac_rate": 1.0,
"beta": 5.0,
"beta_rate": 1.0,
"beta_eta": 0.3,
"filter_radius": 0.9,
"eta": 1.0,
"rho_min": 0.001,
"rho_max": 1.0,
"move_limit": 0.25,
"move_limit_rate": 10.0
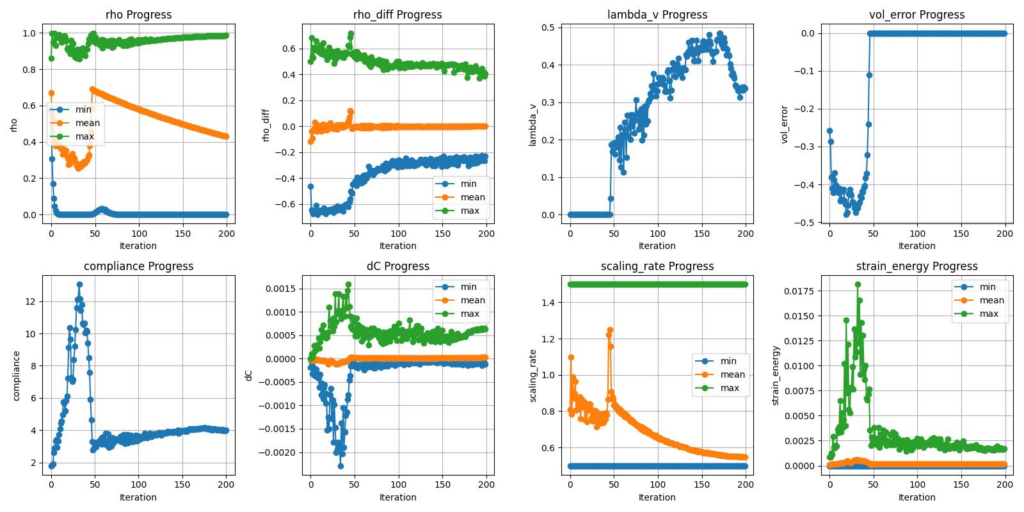
}The progress of optimization and target parameters