Apply Torque Load using Scikit-fem

About

This script solves a basic torsion problem using the finite element method.
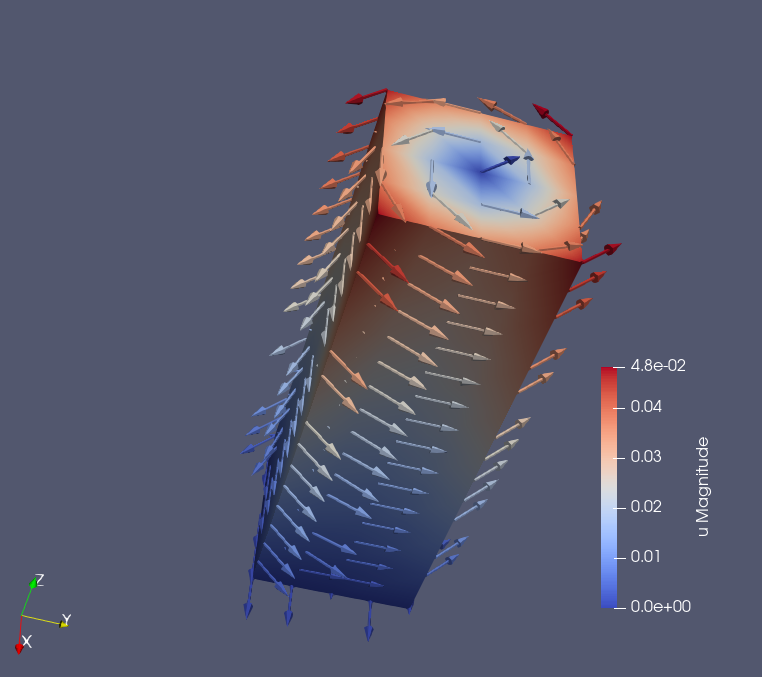
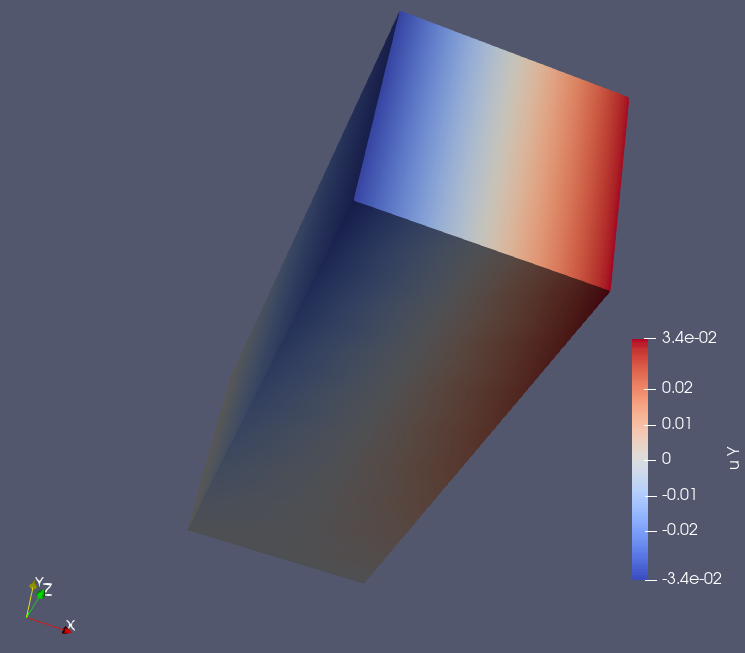
We model a vertical bar, fix its bottom surface, and apply a twisting moment (torque) to the top surface.

First, the code computes geometric properties of the top face—its area, centroid, and polar moment of inertia—so that the applied torque can be converted into an equivalent surface traction. This traction produces the correct twisting effect around the bar’s central axis.

The program then assembles the linear elasticity system, enforces the fixed boundary at the bottom, solves for the displacement field, and finally exports the results for visualization.

Code

import numpy as np
import skfem
from skfem.models.elasticity import linear_elasticity


E = 210e3
nu = 0.3
M_z = 20.0  # Torque [N·mm]

Z_top = 300.0

# ---------------------------
# Fem Mesh and Basis
# ---------------------------
mesh = skfem.MeshTet.init_tensor(
    np.linspace(0.0, 100.0, 3),
    np.linspace(0.0, 100.0, 3),
    np.linspace(0.0, Z_top, 9),
)
mesh = mesh.refined(1)
basis_vec = skfem.Basis(mesh, skfem.ElementVector(skfem.ElementTetP1()))
basis_sca = skfem.Basis(mesh, skfem.ElementTetP1())


def is_top(x):
    return x[2] > Z_top - 1e-9


top_vec = basis_vec.boundary(is_top)
top_sca = basis_sca.boundary(is_top)


# area A = ∫_Γ 1 dS
@skfem.Functional
def area_F(w):
    return 1.0


# The first order m = [∫ x dS, ∫ y dS]
@skfem.Functional
def first_moment_F(w):
    x, y, z = w.x
    return np.array([x, y])


cx = 0.0  # Dummy, overwritten later
cy = 0.0


@skfem.Functional
def polar_moment_F(w):
    x, y, z = w.x
    return (x - cx) ** 2 + (y - cy) ** 2


# ---------------------------
# 1) Computes A, (cx, cy), Jz
# ---------------------------
A = area_F.assemble(top_sca)
m = first_moment_F.assemble(top_sca)
cx = m[0] / A
cy = m[1] / A

print(f"Area A = {A}")
print(f"Center (cx, cy) = ({cx}, {cy})")
Jz = polar_moment_F.assemble(top_sca)

print(f"Polar moment Jz = {Jz}")
alpha = M_z / Jz


# ---------------------------
# 2) Traction (LinearForm)
#    t(x,y) = α * (-(y-cy), (x-cx), 0)
# ---------------------------
# @skfem.LinearForm
# def torque_z(v, w):
#     x, y, z = w.x
#     tx = -alpha * (y - cy)
#     ty = alpha * (x - cx)
#     tz = 0.0
#     return tx * v[0] + ty * v[1] + tz * v[2]

@skfem.LinearForm
def torque_z(v, w):
    x, y, z = w.x
    t = np.array([
        -alpha * (y-cy),
        alpha * (x-cx),
        np.zeros_like(x)
    ])
    return np.einsum('ijk,ijk->jk', t, v)


@skfem.Functional
def torque_z_total(w):
    x, y, z = w.x
    t = np.array([
        -alpha * (y-cy),
        alpha * (x-cx),
        np.zeros_like(x)
    ])
    r = np.array([
        x - cx,
        y - cy,
        np.zeros_like(x)
    ])
    cross = np.cross(r.T, t.T).T
    return cross[2]


f = skfem.asm(torque_z, top_vec)
torque_total = skfem.asm(torque_z_total, top_sca)


print(f"torque_total - setting: {M_z}")
print(f"torque_total - computed: {torque_total}")

# ---------------------------
# 3) Stiffness Matrix & Solve Equation
# ---------------------------
K = skfem.asm(linear_elasticity(E, nu), basis_vec)


def is_bottom(x):
    return x[2] < 1e-9


bottom_dofs = basis_vec.get_dofs(is_bottom).all()
u = skfem.solve(*skfem.condense(K, f, D=bottom_dofs)).reshape(-1, 3)

from sktopt.core import visualization
visualization.export_mesh_with_info(
    mesh,
    point_data_values=[u],
    point_data_names=["u"],
    filepath="./examples/fea/torsion.vtu"
)

Constraints for displacement might be necessary.