Theory
As we mentioned before on that page, QFT circuit is represented as,
\left( \ket{0} + e^{i2\pi 0.j_n} \ket{1} \right) \otimes \left( \ket{0} + e^{i2\pi 0.j_{n-1}j_n} \ket{1} \right) \otimes \cdots \otimes \left( \ket{0} + e^{i2\pi 0.j_1j_2\cdots j_n} \ket{1} \right)So, hadamal gate and general rotation gates are frequently and repeatedly used.
R_l = \begin{pmatrix} 1 & 0 \\ 0 & e^{i\frac{2\pi}{2^l}} \end{pmatrix}Now, we are going to see how to implement that circuit using qiskit
Code
import argparse
import numpy as np
import qiskit
from qiskit import visualization
def qft_simple(qc, num_qubits):
for i in range(num_qubits):
for j in range(i):
qc.cp(
2 * np.pi / (2**(i-j)),
j, i
)
qc.h(i)
return qc
def qft_general(qc, num_qubits):
for j in range(num_qubits):
qc.h(j)
for k in range(j+1, num_qubits):
qc.cp(2 * np.pi / 2**(k-j+1), k, j)
for j in range(num_qubits//2):
qc.swap(j, num_qubits-j-1)
return qc
def main(args):
# initialize circuit
name='ft'
num_qubits = args.qubits_size
qc = qiskit.QuantumCircuit(num_qubits, name=name)
signal = np.ones(2**num_qubits).tolist()
signal = np.array(signal) / np.linalg.norm(signal)
qc.initialize(signal, range(num_qubits))
# define circuit
ft_circuit = qft_general(qc, num_qubits)
print(ft_circuit, len(ft_circuit))
fig = ft_circuit.draw('mpl')
fig.savefig('./circuit-test1.png')
# simulate circuit
simulator = qiskit.Aer.get_backend('statevector_simulator')
compiled_circuit = qiskit.transpile(
ft_circuit,
simulator,
output_name='ft_circuit'
)
job = qiskit.execute(compiled_circuit, simulator)
result = job.result()
statevector = result.get_statevector()
vis1 = visualization.plot_bloch_multivector(statevector)
vis1.savefig('./bloch_multivector-1.png')
# measure state vector
ft_circuit.measure_all()
compiled_meas_circuit = qiskit.transpile(
ft_circuit,
simulator,
output_name='ft_circuit_m'
)
job_meas = qiskit.execute(compiled_meas_circuit, simulator, shots=1024)
result_meas = job_meas.result()
counts = result_meas.get_counts()
vis2 = visualization.plot_histogram(counts)
vis2.savefig('./histogram-1.png')
if __name__ == '__main__':
parser = argparse.ArgumentParser(
description='What this program is going to do.'
)
parser.add_argument(
'--qubits_size', '-QS', type=int, default=4, help=''
)
args = parser.parse_args()
main(args)The Structure of Quantum Circuits
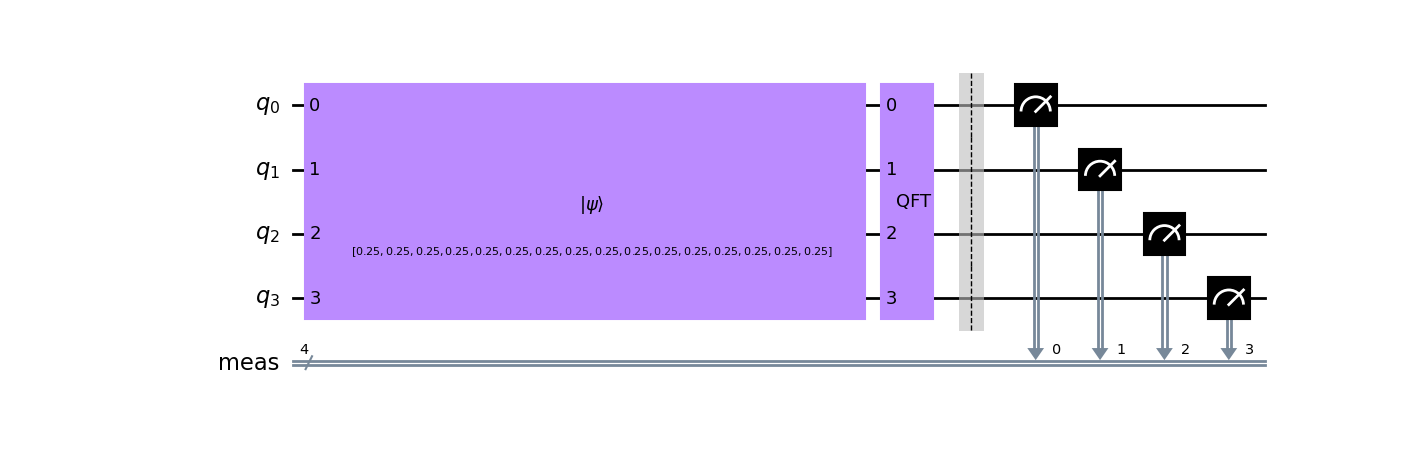
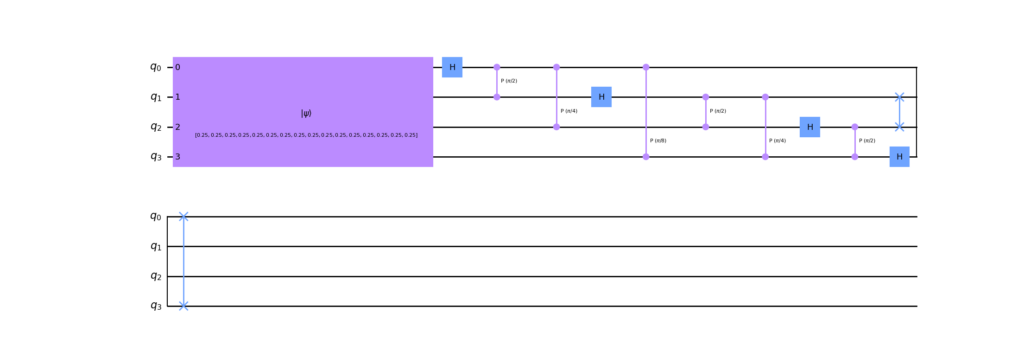
The following illustrates the quantum Fourier transform circuit generated by the code mentioned above. The initial state is Fourier transformed as a vector with constant values.
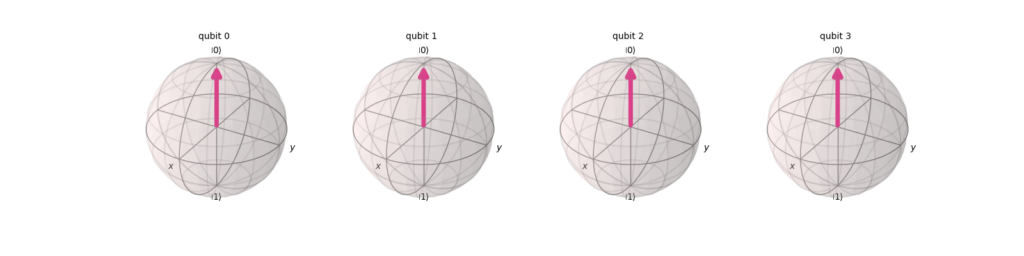
The state vector come out from the circuit
The following represents the state vector after quantum Fourier transformation, depicted on the Bloch sphere. Since a constant value is Fourier transformed, all elements result in the |0⟩ state.
QFT using Qiskit Circuit Library
But actually, we have another simpler implementation using Qiskit Circuit Library, means that Qiskit provides QFT function.
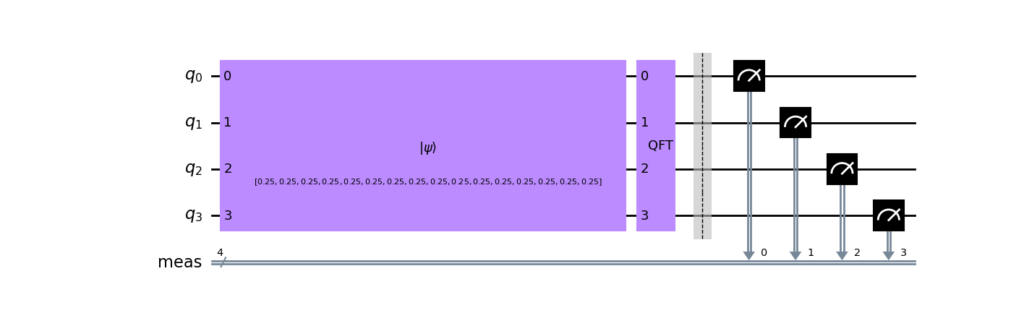
The structure of Quantum Circuit is written as below.
import argparse
import numpy as np
import qiskit
from qiskit import visualization
from qiskit.circuit.library import QFT
def main(args):
num_qubits = args.qubits_size
name='ft'
initial_state = [1/np.sqrt(2**num_qubits)] * 2**num_qubits
qc = qiskit.QuantumCircuit(num_qubits, name=name)
qc.initialize(initial_state, range(num_qubits))
qc.append(QFT(num_qubits), range(num_qubits))
qc.measure_all()
fig = qc.draw('mpl')
fig.savefig('./circuit-test2.png')
simulator = qiskit.Aer.get_backend('statevector_simulator')
compiled_circuit = qiskit.transpile(
qc,
simulator,
output_name='ft_circuit'
)
job = qiskit.execute(compiled_circuit, simulator)
result = job.result()
statevector = result.get_statevector()
vis1 = visualization.plot_bloch_multivector(statevector)
vis1.savefig('./bloch_multivector-2.png')
compiled_meas_circuit = qiskit.transpile(
qc,
simulator,
output_name='ft_circuit2'
)
job_meas = qiskit.execute(compiled_meas_circuit, simulator, shots=1024)
result_meas = job_meas.result()
counts = result_meas.get_counts()
vis2 = visualization.plot_histogram(counts)
vis2.savefig('./histogram-2.png')
if __name__ == '__main__':
parser = argparse.ArgumentParser(
description='What this program is going to do.'
)
parser.add_argument(
'--qubits_size', '-QS', type=int, default=4, help=''
)
args = parser.parse_args()
main(args)Reference
[1] https://github.com/kevin-tofu/qiskit-qft
[2] https://dojo.qulacs.org/en/latest/notebooks/2.3_quantum_Fourier_transform.html