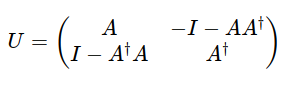To convert any matrix into a unitary matrix, there are several methods, especially used in the context of quantum computing. These methods aim to generate a unitary matrix that can be used in algorithms like Quantum Phase Estimation (QPE) while preserving the properties of the original matrix.
Utilization of Matrix Exponential Function
For any complex matrix A, a unitary matrix U can be generated as U=e^iAt (where t is a real number). The matrix exponential function e^iAt is always unitary and can be implemented in a quantum circuit. This method is commonly used in Hamiltonian simulation.
Use of Schur Complement Matrix
A can be used as part of a Schur complement matrix, forming the following block matrix:
U = \begin{pmatrix}
A & -I - AA^\dagger \\
I - A^\dagger A & A^\dagger
\end{pmatrix}QR decomposition
For a certain matrix ( A ), there is a method which involves performing QR decomposition ( ( A = QR ), where ( Q ) is a unitary matrix and ( R ) is an upper triangular matrix) and using the ( Q ) matrix as the unitary matrix. However, this method requires that ( A ) be a square matrix.