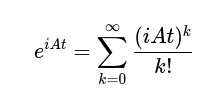QPE looks wonderful, but…
But how do we calculate the eigenvalues of any matrix? I somehow managed to ask ChatGPT. I’m not sure if this is correct. I would be happy if someone who knows the answer could tell me.
Answers from ChatGPT
The process of converting the eigenvalues of a unitary matrix estimated in a quantum circuit back to the eigenvalues of the original non-unitary matrix is not straightforward and often depends on the characteristics of the matrix and the method of transformation. Particularly, when the matrix exponential function ( e^{iAt} ) is used to generate a unitary matrix, there is a specific relationship between the eigenvalues of the original matrix ( A ) and those of the unitary matrix.
When a unitary matrix ( U = e^{iAt} ) is given by quantum phase estimation, the eigenvalues of ( U ) take the form ( e^{i\lambda t} ), where ( \lambda ) are the eigenvalues of ( A ). Using this relationship, it is possible to revert from the eigenvalues of the unitary matrix to those of ( A ).
The process
Specifically, from the eigenvalues ( e^{i\lambda t} ) of the unitary matrix ( U ), the real and imaginary parts of ( \lambda ) can be calculated to determine the eigenvalues of the original matrix ( A ). This is done as follows:
- Determine the phase ( \lambda t ) of the eigenvalue ( e^{i\lambda t} ) of ( U ) using quantum phase estimation.
- To find ( \lambda ) from this phase, divide the phase by ( t ): ( \lambda = \text{phase} / t ).
This method is effective when ( t ) is known in advance. Additionally, if the eigenvalues of ( A ) are complex, the real and imaginary parts can be directly calculated from the phase.
However, this transformation is specific to the case where the unitary matrix is generated using the matrix exponential function, and a different approach may be necessary for unitary matrices generated by other methods. It is also important to note that the accuracy of phase estimation and the choice of ( t ) can affect the precision of the eigenvalues.
具体的には、ユニタリ行列 \( U \) の固有値 \( e^{i\lambda t} \) から、\( \lambda \) の実部と虚部を計算することにより、オリジナルの行列 \( A \) の固有値を求めることができます。これは次のように行います:
1. \( U \) の固有値 \( e^{i\lambda t} \) の位相 \( \lambda t \) を量子位相推定で求めます。
2. この位相から \( \lambda \) を求めるために、位相を \( t \) で割ります:\( \lambda = \text{位相} / t \)。
この方法は、\( t \) が事前に知られている場合に有効です。また、\( A \) の固有値が複素数である場合、実部と虚部は位相から直接計算することができます。
ただし、この変換は行列指数関数を使用してユニタリ行列を生成する場合に特有のものであり、他の方法でユニタリ行列を生成した場合は、異なるアプローチが必要になる可能性があります。また、位相推定の精度や \( t \) の選択が固有値の精度に影響を与えることにも注意が必要です。matrix exponential function?
Here is the definition
e^A = \sum_{k=0}^{\infty} \frac{A^k}{k!}This infinite series converges for any square matrix, and the result is again a square matrix. The matrix exponential function is particularly important in various mathematical and physical contexts, such as solving differential equations, quantum mechanics, and control theory.
The time extension of exponential function
The definition of the matrix exponential function eiAt extends the concept of the matrix exponential function for a matrix A and a real number t. This function is defined by the following infinite series:
e^{iAt} = \sum_{k=0}^{\infty} \frac{(iAt)^k}{k!}Here, i is the imaginary unit, A is any square matrix, and t is a real number.(iAt)k denotes the k-th power of the matrix iAt, and !k! represents the factorial of k.
This formula uses the general definition of the matrix exponential function and plays a crucial role particularly in the fields of quantum mechanics and quantum computing. When the matrix A represents a Hamiltonian (a matrix that represents energy), eiAt is interpreted as a time-evolution operator, describing the temporal evolution of the system.
How to decide t to compute phase by QPE (from ChatGPT)
任意の行列 \( A \) の固有値を推定する際に行列指数関数 \( e^{iAt} \) の時間発展形式を使用する場合、時間 \( t \) の選択は重要です。適切な \( t \) の選択は、量子位相推定アルゴリズムの精度と効率に大きく影響します。以下に、\( t \) を決定する際の考慮点をいくつか挙げます:
1. **精度の向上**:\( t \) が大きいほど、位相推定の精度が向上します。これは、\( e^{iAt} \) の固有値 \( e^{i\lambda t} \) の位相 \( \lambda t \) が大きくなり、より細かい差異を検出しやすくなるためです。ただし、\( t \) が大きすぎると、量子位相推定で必要となる量子ビット数が増え、量子回路が複雑になります。
2. **アルゴリズムの制約**:量子位相推定アルゴリズムの性質と制約に基づき、\( t \) を選択する必要があります。特に、使用する量子コンピュータのコヒーレンス時間やゲートのエラー率を考慮する必要があります。
3. **実装の実用性**:量子回路の実装において、実用的に実行可能な範囲内で \( t \) を選択することが重要です。量子ゲートの数や回路の深さに限界があるため、これらの制約内で最適な \( t \) を選ぶ必要があります。
4. **行列 \( A \) の特性**:行列 \( A \) の固有値の範囲や特性に基づいて、\( t \) を調整することも重要です。固有値の範囲が広い場合、それに適応するよう \( t \) を調整する必要があります。
実際には、これらの要因をバランスさせながら、試行錯誤や実験を通じて最適な \( t \) を見つけることが一般的です。理論的な分析と実験的な検証の両方を組み合わせることで、最も効率的で精度の高い \( t \) を決定することができます。