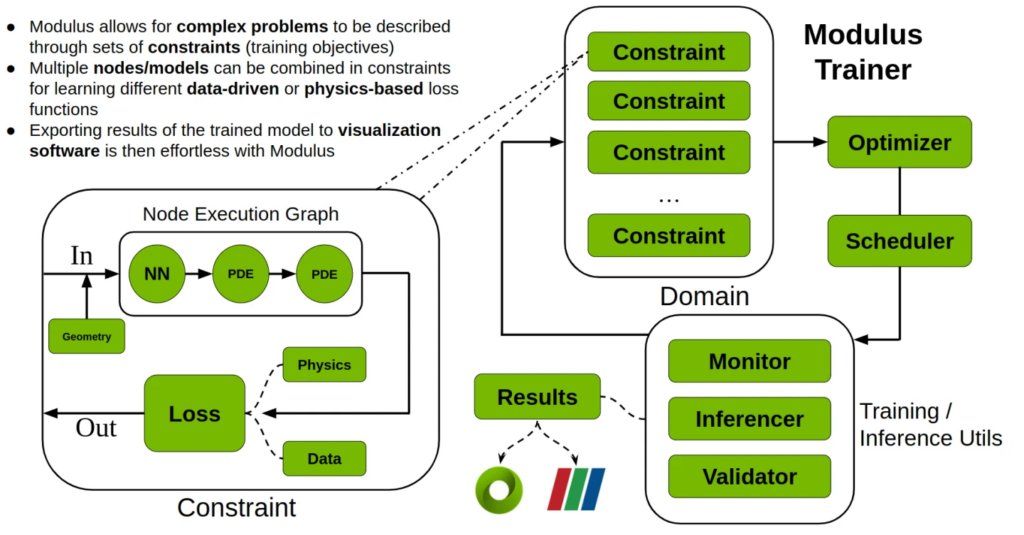
Overview
Nvidia is developing Neural Networks training tool for Physics. Here shows what functions it has
https://docs.nvidia.com/deeplearning/modulus/modulus-v2209/user_guide/basics/modulus_overview.html
Neural Netork Models
As we can see above articles, it seems that there are primary 2 types of neural network series
- Physics Informed Neural Network(PINN)
PINN (Physics Informed Neural Networks) is a method where a neural network is trained to output solutions to partial differential equations (PDEs) for inputs at points in space, known as Collocation Points. Consequently, the output must satisfy the given partial differential equations. The core idea is to use automatic differentiation of the neural network to compute the partial differential loss and to train the network to minimize this loss. This approach effectively integrates the constraints of the PDEs into the learning process of the neural network. In addition to learning the solutions to partial differential equations, the training in PINN (Physics Informed Neural Networks) also involves ensuring that the network satisfies constraints such as boundary conditions. This means that the neural network not only learns to approximate the solutions of the PDEs but also adheres to the specified physical constraints and boundary conditions of the problem, which are crucial for the accuracy and applicability of the model in real-world scenarios.
- Neural Operator
While Physics Informed Neural Networks (PINN) optimize a neural network for a specific partial differential equation (PDE), the approach of Neural Network Operators involves learning how to solve PDEs through supervised learning. However, this learning is not done for a specific partial differential equation, but rather for a general form of a PDE. This means the learning process involves a wide range of problems that have the same formal structure but different coefficients. The aim of this approach is to train a model that can solve a more general class of partial differential equations, enhancing its versatility and applicability across various scenarios.
PDEs
There are many PDEs prepared.

>>> from modulus.eq.pdes.navier_stokes import NavierStokes
>>> ns = NavierStokes(nu=0.01, rho=1, dim=2)
>>> ns.pprint()
continuity: u__x + v__y
momentum_x: u*u__x + v*u__y + p__x + u__t - 0.01*u__x__x - 0.01*u__y__y
momentum_y: u*v__x + v*v__y + p__y + v__t - 0.01*v__x__x - 0.01*v__y__yConstructive Solid Geometry
It appears that there is functionality for generating shapes by combining simple forms.