I forgot where I found this. What weird of this paper is that it is written by anonymous writers.
https://openreview.net/pdf?id=40Mw2GJnlZ
Strong BCC
Unlike the typical PINN model (a simple linear feedforward), they introduce the Strong BC PINN. This is a model that incorporates boundary conditions into the equations, as shown below. Therefore, while the typical PINN requires simultaneous optimization of both BC and PDE loss, this is not necessary for the Strong BC PINN.

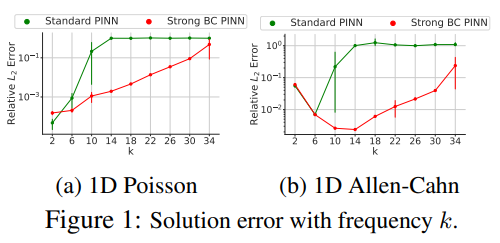
Compared to the typical PINN model, the Strong BC PINN appears to function better in learning high-frequency components.
Fourier PINNs
The Strong BC PINN is limited to specific boundary conditions, such as Dirichlet conditions, which significantly restricts its applicability. To overcome these issues, we are inspired by our analysis and propose the Fourier PINN. This is a simple, general, yet powerful method that can handle various boundary conditions like the standard PINN.
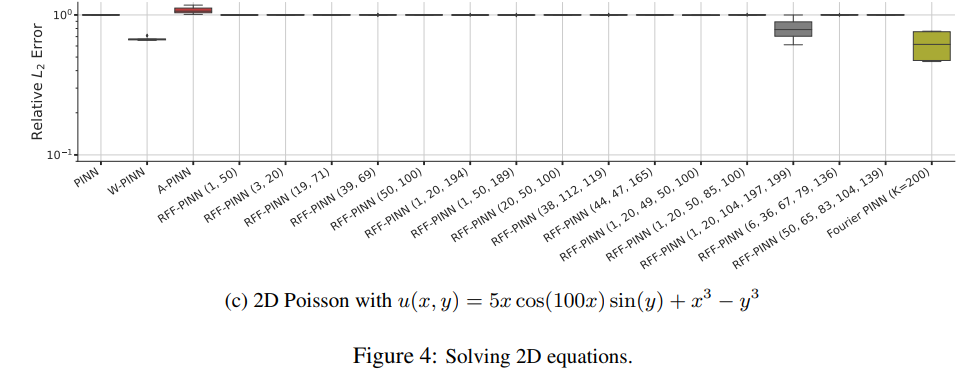
Experiments