About
The Variational Quantum Eigensolver (VQE) is an algorithm that operates on quantum computers and is used for optimization problems to find the ground state energy (likely used in physics and chemistry calculations). This algorithm employs a hybrid approach of quantum and classical computing. As a result, it seems suitable for noisy intermediate-scale quantum (NISQ) devices. Once a Hamiltonian is designed, it appears to have high versatility due to its operational capability.
https://arxiv.org/pdf/1304.3061.pdf
Variational Principle
What is Variational Principle?
When the Hamiltonian ( H ) of a system is given, the energy expectation value ( E ) for any state ( psi ) of that system is expressed as follows:
E = \bra{\psi} H \ket{\psi}\geq E_{0}above E0 is minimal eigen value of hamiltonian H. This is so called Variational Principle.
At this time, any vector can be represented as a superposition of eigen vectors.
\ket{\psi}=\sum_{k=0}^{N-1}{C_k\ket{E_k}}
Therefore, the following formulation holds true for any psi.
\bra{\psi} H \ket{\psi}=[\sum_{k=0}^{N-1}{C_k^*\bra{E_k}}]H[\sum_{k=0}^{N-1}{C_k\ket{E_k}}]\\
=\sum_{k=0}^{N-1}{|C_k|^2E_k}\geq E_{0}Optimization
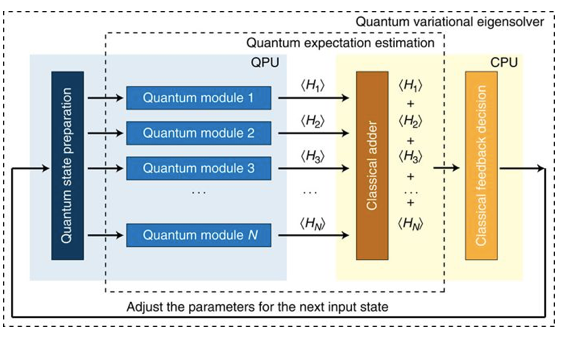
As VQE evaluate E for different psi until E becomes minimal, according to the variational principle, any estimate will approach the minimum value. And by using psi with parameter theta, VQE compute the theta that minimizes Hamiltonian H through optimization on a classical computer (such as gradient descent, for example).
i.e. VQE is algorithm that repeats evaluation for measuring H, and infers psi( to decide theta).
Ansats
Reference
[1] https://arxiv.org/abs/1304.3061
