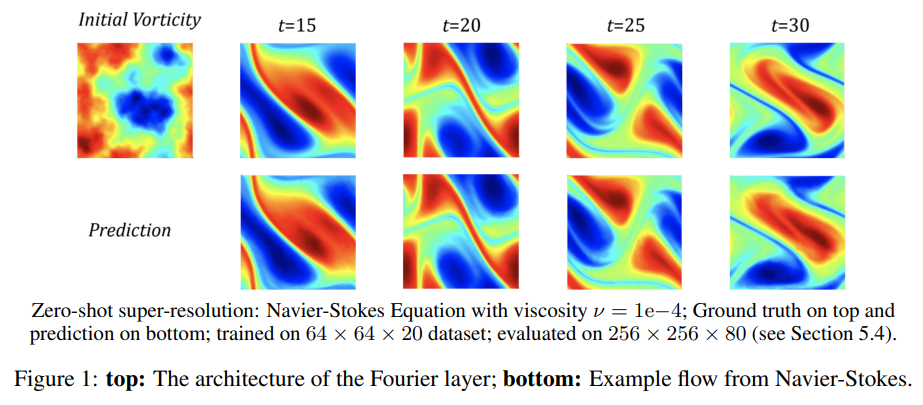
Navier-Stokes
There are many ways to represent this equation.
Polite Form to represent(Looks redundant)
\begin{align*}
\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} &= -\frac{1}{\rho}\frac{\partial p}{\partial x} + \frac{\mu}{\rho}\left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}\right) + f_x \\
\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} &= -\frac{1}{\rho}\frac{\partial p}{\partial y} + \frac{\mu}{\rho}\left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2}\right) + f_y \\
\frac{\partial w}{\partial t} + u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z} &= -\frac{1}{\rho}\frac{\partial p}{\partial z} + \frac{\mu}{\rho}\left(\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2}\right) + f_z
\end{align*}p is the pressure, ρ is the density of the fluid, μ is the dynamic viscosity coefficient
Simple Form
\frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla)\mathbf{v} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{v} + \mathbf{f}\nabla^2 = \nabla \cdot \nabla = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}A Form using grad and div
\frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \text{grad})\mathbf{v} = -\frac{1}{\rho} \text{grad} p + \mathbf{v} \text{ div(grad } \mathbf{v}) + \mathbf{f} \\
\text{grad } A = \begin{pmatrix}
\frac{\partial A}{\partial x} \\
\frac{\partial A}{\partial y} \\
\frac{\partial A}{\partial z}
\end{pmatrix} = \nabla A \\
\text{div } \mathbf{V} = \frac{\partial V_x}{\partial x} + \frac{\partial V_y}{\partial y} + \frac{\partial V_z}{\partial z} = \nabla \cdot \mathbf{V}
Reference
Thanks.
https://qiita.com/US3/items/1c306bec5a50cd8874ce