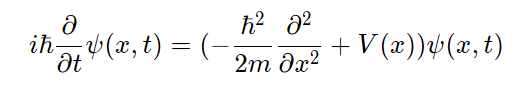Knowing several key elements can make the concept easier to understand.
Principle of Superposition
The principle of superposition states that for a linear homogeneous equation, solutions can be superimposed. In other words, if the solution of a certain equation is A or B, then aA+bB is also a solution to that equation. This fact implies that in investigating the properties of equations that may have complex solutions, it suffices to consider only simple functions. In the context of the Schrödinger equation, understanding this concept is facilitated by simple triangular waves.
You can use below the simplest wave function as solution.
\begin{align}
\psi=e^{2{\pi}i({x\over\lambda}-{\nu}t)}
\end{align}Eigenvalue Equations
Eigenvalue equations are akin to the relationship between eigenvalues/eigenvectors in matrices. When an operator is multiplied by a function, it yields a value obtained by multiplying the function by a scalar value. In quantum mechanics, obtaining physical quantities involves multiplying operators to obtain physical quantities (scalar values).
For example, the spatial derivative in the one-dimensional Schrödinger equation represents momentum, while the temporal derivative represents energy.
\begin{align}
-i\hbar\frac{\partial}{\partial{x}}\psi=-i\hbar\frac{\partial}{\partial{x}} e^{2{\pi}i({x\over\lambda}-{\nu}t)} = \frac{h}{\lambda}e^{2{\pi}i({x\over\lambda}-{\nu}t)}\\
i\hbar\frac{\partial}{\partial{t}}\psi=i\hbar\frac{\partial}{\partial{t}} e^{2{\pi}i({x\over\lambda}-{\nu}t)} = h\nu {e^{2{\pi}i({x\over\lambda}-{\nu}t)}}\\
\end{align}Energy Conservation
The energy of a wave is equal to the sum of its kinetic energy and the potential field. This representation is actually, as same as classic physics formulation.
\begin{align}
E=H=\frac{p^2}{2m}+V
\end{align}These energies can be obtained using operators as shown earlier using observable operators. Specifically, the energy of the wave is
\begin{align}
E=i\hbar\frac{\partial}{\partial{t}}\psi(x, t)
\end{align}Similarly, the kinetic energy is obtained by applying the appropriate operator to the wave function.
\begin{align}
-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial{x^2}}\psi(x, t)
\end{align}Combining equations (5) and (6) with the potential field yields the one-dimensional Schrödinger equation:
\begin{align}
i\hbar\frac{\partial}{\partial{t}}\psi(x, t)=(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial{x^2}}+V(x))\psi(x, t)
\end{align}