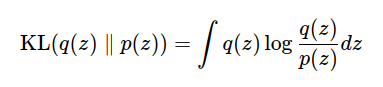About
Evidence Lower Bound (ELBO) is a fundamental concept in variational inference, a technique used for approximating complex probability distributions in Bayesian statistics. It revolves around the idea of optimizing a simpler distribution to approximate a more complex one, particularly in contexts where exact inference is computationally infeasible. ELBO is especially useful when considering loss functions between distributions in models like Variational Autoencoders (VAEs) or Gaussian processes.
Our goal is to model the data distribution p(\mathbf{X}) and approximate it using latent variables. If the latent variable \mathbf{Z} follows a simple distribution like a Gaussian, this model can be regarded as a Gaussian Mixture Model consisting of integrated (or accumulated) simple models.
p(\mathbf{X}) = \int p(\mathbf{X} | \mathbf{Z}) p(\mathbf{Z}) \, d\mathbf{Z}However, the problem is that we cannot directly observe \mathbf{Z}. Therefore, we need to estimate the distribution of \mathbf{Z}. Additionally, as we acquire more data, the shape of the distribution may change, making direct computation difficult. Hence, we use an approximation function.
The Evidence Lower Bound (ELBO) and Variational Inference
The goal is to approximate the posterior distribution p(\mathbf{Z} | \mathbf{X}) with an approximate distribution q(\mathbf{Z} | \mathbf{X}), where \mathbf{Z} is the latent variable and \mathbf{X} is the data. Let’s consider Bayes’ rule:
p(\mathbf{Z} | \mathbf{X}) = \frac{p(\mathbf{X} | \mathbf{Z}) p(\mathbf{Z})}{p(\mathbf{X})}But computing p(\mathbf{X}) requires integrating over all possible \mathbf{Z} , which is often computationally intractable:
p(\mathbf{X}) = \int p(\mathbf{X} | \mathbf{Z}) p(\mathbf{Z}) \, d\mathbf{Z}Variational inference addresses this by choosing a simpler, parameterized distribution q(\mathbf{Z} | \mathbf{X}) and optimizing its parameters to closely approximate p(\mathbf{Z} | \mathbf{X}) :
p(\mathbf{Z} | \mathbf{X}) \approx q(\mathbf{Z} | \mathbf{X})Variational inference avoids direct computation of p(\mathbf{X}) by maximizing the ELBO, which is derived from the log-evidence:
\begin{align}
\log p(\mathbf{X}) &= \log \int p(\mathbf{X}, \mathbf{Z}) \, d\mathbf{Z} \\
&= \log \int q(\mathbf{Z} | \mathbf{X}) \frac{p(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z} | \mathbf{X})} \, d\mathbf{Z} \\
&= \log \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \frac{p(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z} | \mathbf{X})} \right]
\end{align}Applying Jensen’s inequality:
\log \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \frac{p(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z} | \mathbf{X})} \right] \geq \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log \frac{p(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z} | \mathbf{X})} \right]\\
\log p(\mathbf{X}) \geq \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log p(\mathbf{X}, \mathbf{Z}) - \log q(\mathbf{Z} | \mathbf{X}) \right] = \text{ELBO}Kullback-Leibler Divergence
The concept of Kullback-Leibler Divergence (KL Divergence), which measures the “distance” between two probability distributions, is crucial for understanding ELBO. When approximating p(\mathbf{Z} | \mathbf{X}) with q(\mathbf{Z} | \mathbf{X}), the KL divergence is:
\text{KL}(q(\mathbf{Z} | \mathbf{X}) \parallel p(\mathbf{Z} | \mathbf{X})) = \int q(\mathbf{Z} | \mathbf{X}) \log \frac{q(\mathbf{Z} | \mathbf{X})}{p(\mathbf{Z} | \mathbf{X})} \, d\mathbf{Z}Using Bayes’ theorem to rewrite \log p(\mathbf{Z} | \mathbf{X}) :
\log p(\mathbf{Z} | \mathbf{X}) = \log p(\mathbf{X}, \mathbf{Z}) - \log p(\mathbf{X})Substituting back into the KL divergence:
\begin{align}
\text{KL}(q(\mathbf{Z} | \mathbf{X}) \parallel p(\mathbf{Z} | \mathbf{X})) &= \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log q(\mathbf{Z} | \mathbf{X}) - \log p(\mathbf{Z} | \mathbf{X}) \right] \\
&= \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log q(\mathbf{Z} | \mathbf{X}) - \log p(\mathbf{X}, \mathbf{Z}) + \log p(\mathbf{X}) \right]
\end{align}Since \log p(\mathbf{X}) is constant with respect to \mathbf{Z} :
\text{KL}(q(\mathbf{Z} | \mathbf{X}) \parallel p(\mathbf{Z} | \mathbf{X})) = \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log q(\mathbf{Z} | \mathbf{X}) - \log p(\mathbf{X}, \mathbf{Z}) \right] + \log p(\mathbf{X})\\
\log p(\mathbf{X}) = \text{ELBO} + \text{KL}(q(\mathbf{Z} | \mathbf{X}) \parallel p(\mathbf{Z} | \mathbf{X}))Since the KL divergence is always non-negative ( \text{KL}(\cdot) \geq 0 ):
\begin{align}
\log p(\mathbf{X}) \geq \text{ELBO}
\end{align}This shows that ELBO is a lower bound of the log-evidence \log p(\mathbf{X}) .
Interpretation of ELBO
ELBO takes a value which is slightly lower value than log p(X)
\begin{align}
\log p(x) = \text{ELBO} + \text{KL}(q(z) \parallel p(z | x))\\
\log p(x) \geq \text{ELBO}
=\mathbb{E}_{q(z)}[\log p(x | z)] - \text{KL}(q(z) \parallel p(z))
\end{align}ELBO can be expressed as:
\begin{align}
\text{ELBO} &= \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log p(\mathbf{X}, \mathbf{Z}) - \log q(\mathbf{Z} | \mathbf{X}) \right] \\
&= \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log p(\mathbf{X} | \mathbf{Z}) \right] + \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log p(\mathbf{Z}) - \log q(\mathbf{Z} | \mathbf{X}) \right]
\end{align}
This consists of two terms:
- Reconstruction Term (Expected Log-Likelihood): \mathbb{E}_{q(\mathbf{Z} | \mathbf{X})} \left[ \log p(\mathbf{X} | \mathbf{Z}) \right] This measures how well the model can reconstruct the data \mathbf{X} from the latent variables \mathbf{Z} .
- Regularization Term (Negative KL Divergence): \text{KL}(q(\mathbf{Z} | \mathbf{X}) \parallel p(\mathbf{Z}). This encourages the approximate posterior q(\mathbf{Z} | \mathbf{X}) to be close to the prior p(\mathbf{Z}), helping to prevent overfitting.
What does this formulation mean?
By maximizing the ELBO, we effectively minimize the KL divergence between q(\mathbf{Z} | \mathbf{X}) and the true posterior p(\mathbf{Z} | \mathbf{X}). This leads to:
- Improved Data Reconstruction: Maximizing the expected log-likelihood ensures the model can accurately reconstruct the data.
- Better Generalization: Minimizing the KL divergence between q(\mathbf{Z} | \mathbf{X}) and p(\mathbf{Z}) regularizes the model, promoting better generalization to unseen data.
In essence, ELBO serves as both a tool for inference and a loss function to optimize our model, balancing reconstruction accuracy and model complexity.
Why is ELBO used?
At a glance, both KL divergence in log p(x) looks quite similar.
\begin{align}
\text{KL}(q(z) \parallel p(z | x))\\
\text{KL}(q(z) \parallel p(z))
\end{align}But optimizing (11) is difficult or impossible since it needs marginalization of p(x) to compute the posterior, wheareas it is possible to compute p(z) and q(z) since it is a simple distribution.
- (11) is a theoretical value that indicates the difference between the approximate posterior distribution and the true posterior distribution. If it is closer to 0, the approximation is better.
- (12) acts as a regularizer to reduce model complexity and prevent overfitting
Reference
https://yunfanj.com/blog/2021/01/11/ELBO.html