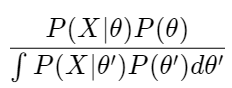Stochastic Modeling
To modeling data distributions, there are some useful Probabilistic Distributions are used. To summarize these distributions, I write down some of it by referring [1]. I think what important is to understand
- What kind of distributions are suitable for specific datasets
- Relation or Characteristic of distribution. Especially, conjugate priors are important for getting analytical calculus.
Bernoulli distribution
The Bernoulli distribution is a simple discrete distribution having only two possible outcomes, commonly termed as success and failure (1 and 0). It is used to model experiments that can result in just two outcomes and has a single parameter p, which represents the probability of success.
Bernoulli(x | \pi)=\pi^x(1-\pi)^{1-x}Binomial Distribution
The binomial distribution extends the Bernoulli distribution to multiple trials. It represents the probability of obtaining a fixed number of successes in a fixed number of independent trials of a Bernoulli experiment. We should use when we focus on number of 1 emerging (, which is k in this case) in this trials.
Bi(k|\pi, n) = \binom{n}{k} \pi^k (1-\pi)^{n-k}Poisson Distribution
The Poisson distribution is used to describe the distribution of discrete events, such as frequencies. For example, it is used to model the probability of occurrence of rare phenomena.
\begin{align}
Po(x|\lambda)=\frac{\lambda^x}{x!}e^{-\lambda}\\
E[Po]=\lambda\\
V[Po]=\lambda
\end{align}Poisson is relevant to Binomial Distribution actually. If the number of trial get infinite, and its probability is low, it would get close to.
Multinomial Distribution
Binomial Distribution is extended to in the case of multi variable, it is called multinomial distribution
Beta Distribution
This is prior distribution of binomial distribution. So it is used for solving priori distribution of binomial distribution.
The Beta distribution is a continuous probability distribution with parameters α and β, which models the distribution of a probability variable (e.g., the probability of success) that takes values between 0 and 1. The Beta distribution represents the belief that ‘success’ has been observed α−1 times and ‘failure’ β−1 times. The PDF of the Beta distribution is,
Beta(x| \alpha, \beta) = \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)}B is called the Beta function and is used as a normalization constant for continuous probability distributions. Within this, the Gamma function can be considered as a generalization of the factorial.
\begin{align}
B(\alpha, \beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)}\\
\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt\\
\Gamma(z+1) = z \Gamma(z)
\end{align}Anyway, the expectation and variance of the Beta distribution are
\begin{align}
E[Beta]=\frac{a}{a+b}\\
V[Beta]=\frac{ab}{(a+b)^2(1+a+b)}
\end{align}Dirichlet Distribution
Dirichlet Distribution is an extension of Beta Distribution using multi-variable. As same as Beta Distribution, this distribution is prior of multinomial distribution. By using the Dirichlet, posterior of multinomial is gotten. it means that Dirichlet (and Beta) Distribution is conjugate priors.
This distribution has K positive parameters α1,α2,…,αK, corresponding to the observed counts for each category in a multinomial distribution. The PDF of the Dirichlet distribution is,
p(x_1, \ldots, x_K| \alpha_1, \ldots, \alpha_K) = \frac{1}{B(\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}Anyway, the expectation and variance of the Dirichlet distribution are
\begin{align}
E[Di(x_k)]=\frac{\alpha_k}{\alpha_0}\\
V[Di(x_k)]=\frac{\alpha_k(\alpha_0-\alpha_k)}{(\alpha_0)^2(1+\alpha_0)}\\
\alpha_0 = \sum_{i=1}^n \alpha_i
\end{align}Reference
[1] Non-Parametric Bayse 佐藤一誠