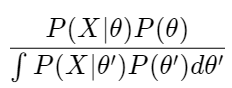As we can see in a article(https://eye.kohei-kevin.com/2024/04/20/review-map-mle-bayes-estimation/) (which I posted before), MCMC algorithms are used for do bayes estimation. Generally there are 2 ways of the Bayes estimation using MCMC, Metropolis-Hastings and Gibbs Sampling. I will summarize these two methods and its difference.
The difference
- Proposal Distribution: In Metropolis-Hastings, any proposal distribution can be used, whereas in Gibbs sampling, the proposal distribution is automatically the conditional distribution of the component being sampled.
- Acceptance Probability: Metropolis-Hastings requires an acceptance step, but in Gibbs sampling, every proposal is accepted with probability 1 because it follows the conditional distribution directly.
Metropolis-Hastings
The Metropolis-Hastings algorithm uses a proposal distribution “q” to suggest the next state and accepts or rejects this proposal with a certain acceptance probability. This can be expressed with the following steps:
\begin{align*}
\textbf{1. Proposal Step:} & \\
\text{From the current state } x^{(t)}, & \\
\text{generate a new state } x' \text{ using the proposal distribution } q(x' \mid x^{(t)}). & \\
\textbf{2. Acceptance Step:} & \\
\text{Compute the acceptance probability } \alpha(x^{(t)}, x'): & \\
\alpha(x^{(t)}, x') = \min\left(1, \frac{p(x') \, q(x^{(t)} \mid x')}{p(x^{(t)}) \, q(x' \mid x^{(t)})}\right) & \\
\text{where } p(x) \text{ is the target distribution.} & \\
\textbf{3. Update Step:} & \\
\text{Generate a uniform random number } u \sim \text{Uniform}(0, 1), & \\
\text{and if } u \leq \alpha(x^{(t)}, x'), \text{ set } x^{(t+1)} = x'; & \\
\text{otherwise, } \text{ set } x^{(t+1)} = x^{(t)}. &
\end{align*}Gibbs Sampling
Gibbs sampling is a method for sequentially sampling each component of a multi-dimensional random variable from its conditional distributions.
Suppose you have a multi-dimensional random variable
\mathbf{x} = (x_1, x_2, \ldots, x_n)In Gibbs sampling, each component is updated sequentially. For the i-th component, fix all other components x−i and sample xi from the conditional distribution:
x_i \sim p(x_i \mid \mathbf{x}_{-i})This process is repeated for each component, cycling through the vector x repeatedly to generate a sequence of samples approximating the joint distribution.