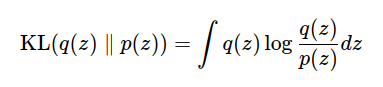Reasoning the result from machine learning models is one of the most demanded task from business side since it is quite difficult to know whether the model is well trained or not. In this article, I introduce a method that can be explainable and have good capabilities of fitting. The baseline model is Gaussian Process, which is well known interpretable model even if as it is, since it is using probabilistic model. But original model doesn’t have properties to know how much contribution the explanatory variables have for prediction.
The paper that I am going to introduce is here, Yuya Yoshikawa, Tomoharu Iwata in https://arxiv.org/abs/2007.01669
https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9646444
About
While searching for a more explainable approach to Gaussian Process algorithms, I came across the paper titled “GAUSSIAN PROCESS REGRESSION WITH LOCAL EXPLANATION.” Published two years ago in 2022, this paper provides valuable insights, though there have been more recent developments in the field, such as, Kurt Butler, Guanchao Feng, Petar M. Djuric, “Explainable Learning with Gaussian Processes” https://arxiv.org/abs/2403.07072. But I found that this paper’s idea looks quite simple and smart, and well analyzed and experimented with some GP algorithms on datasets. And the derivation looks beautiful. So, I prefer this paper rather than one that is published recently.
Anyway, what they suggested is that local linear regression using GP, called “GPX”.
GPX?
Their formulation looks simple, but good idea(I haven’t understood in detail though. I would like to ask them…). Anyway, what we want is “explainable” GP model. So their approach is that the model is going to generate weights for linear regression model in order to make its predictions explainable. Let’s say we have simple linear regression model like below.
y=w^Tx+n
Here, w is weight vector, x is input vector and n is noise vector. Just by seeing the magnitude of weight in an vector or an element in elementwise product wx, we can distinguish which weight or input contribute to the prediction, y.
What if we could get weight vector dynamically based on input? The local weights based on input x tells us contribution for prediction, meaning that is explainable. So, idea is to get a local weight vector from explanatory variable (input) using Gaussian Process.
\begin{align}
w_i = g(x_i) + \epsilon_w\\
g(x) = \left( g_1(x), g_2(x), \ldots, g_d(x) \right)\\
g_l(x) \sim \text{GP}(m(x), k_\theta(x, x'))
\end{align}Where m is mean function and k is kernel function.
Since the model seems like Hidden Markov, this model can be represented as Graphical Model.
Optimization
Marginal likelihood
The marginal likelihood is derieved by integrating out G and W.
\begin{align}
p(y | X, Z) = \int \int p(y, W, G | X, Z) \, dW \, dG \\
= \mathcal{N}(y | 0, C)\\
where \space C = \sigma^2_y I_n + \bar{Z} \bar{K} + \sigma^2_w I_n \bar{Z}\\
= \sigma^2_y I_n + (K + \sigma^2_w I_n) \bar{Z} \bar{Z}^{\top}.
\end{align}Negative Log Likelihood
To train the model, the negative log likelihood(NLL) is computed. As we can see above, the marginal likelihood is Gaussian
Distribution.
\begin{align}
p(\mathbf{x}|\boldsymbol{0}, \boldsymbol{C}) = \mathcal{N}(y | 0, C)\\
= \frac{1}{(2\pi)^{d/2} |\boldsymbol{C}|^{1/2}}
\exp\left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{0})^T \boldsymbol{C}^{-1} (\mathbf{x} - \boldsymbol{0})\right)
\end{align}The negative log likelihood is computed as follows:
\begin{align}
\text{NLL} = -\log \prod_{i=1}^{n} p(\mathbf{y}_i|\boldsymbol{0}, \boldsymbol{C})\\
= -\log \left( \frac{1}{(2\pi)^{nd/2} |\boldsymbol{C}|^{n/2}} \exp\left(-\frac{1}{2} \sum_{i=1}^{n} (\mathbf{y}_i - \boldsymbol{0})^T \boldsymbol{C}^{-1} (\mathbf{y}_i - \boldsymbol{0}) \right) \right)\\
= \frac{nd}{2} \log(2\pi) + \frac{n}{2} \log|\boldsymbol{C}| + \frac{1}{2} \sum_{i=1}^{n} \mathbf{y}_i^T \boldsymbol{C}^{-1} \mathbf{y}_i
\end{align}Taking gradients of above NLL for parameters, gradients descent based method which is L-BFGS, is conducted.
Evaluation and Comparison
Since I haven’t seen a paper in the field of explainable AI ,I was not sure how to evaluate models. But their paper clearly shows some metrics for explainability. This would be good reference for study. They evaluate their model and the others in terms of
- Accuracy: How accurate is the prediction of the interpretable model?
- Faithfulness: Are feature contributions indicative of “true” importance?
- Sufficiency: Do k-most important features reflect the prediction?
- Stability: How consistent are the explanations for similar or neighboring examples?
in mathematical way.
Their approach is one of the best among the models that they evaluated.
Implementation
Thankfully, they open their official code. It is implemented on GPytorch, which is one of the most popular GP library, it looks beautiful.
https://github.com/yuyay/gpx?tab=readme-ov-file