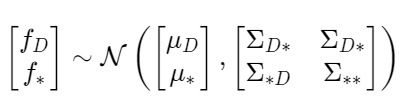About
Ridge regression is a linear regression method that estimates weight parameters based on a nonlinear function basis. Note that we assume the normal distribution as the prior distribution of the weight parameters. This concept is used in Gaussian Process, so I will summarize briefly.
Modeling
The prediction model is simply described as
\begin{align}
y = \Phi(x) w \\
\Phi(x) = \begin{bmatrix}
\phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_H(x_1) \\
\phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_H(x_2) \\
\vdots & \vdots & \ddots & \vdots \\
\phi_1(x_n) & \phi_2(x_n) & \cdots & \phi_H(x_n)
\end{bmatrix}
\end{align}x is d-dimensional vector, H is the number of features and n is number of data.
The prior of weight values is described as Normal Distribution (3)
\begin{align}
w \sim \space \N(0, \lambda I)
\end{align}Since weight is gaussian distribution, the distribution of y is also gaussian distribution, y is gotten from linear transform.
\Sigma=E [y^Ty]=E[(\Phi(x) w)^T(\Phi(x) w)]\\ =\Phi(x)^T E[w^T w]\Phi(x)=\lambda^2 \Phi(x)^T\Phi(x)\\ w \sim \space \N(0, \lambda^2 \Phi(x)^T\Phi(x))
Posterior of Weight Vector
The posterior of weight w given y is
p(w | \mathbf{y}, \Phi) \propto p(\mathbf{y} | \Phi, w) p(w)
As we can see above, the distribution of y and w is proportional to
\begin{align}
p(\mathbf{y} | \Phi, w) \propto \exp\left(-\frac{1}{2} (\mathbf{y} - \Phi w)^T (\mathbf{y} - \Phi w)\right)\\
p(w) \propto \exp\left(-\frac{1}{2\lambda} w^T w\right)
\end{align}Using (4), (5), the w is analytically gotten
w = (\Phi^T \Phi + \frac{1}{\lambda} I)^{-1} \Phi^T \mathbf{y}