About
Optimal Quantum Circuits for General Two-Qubit Gates
Magic Basis
\begin{align}
M = \frac{1}{\sqrt{2}}\begin{pmatrix}
1& i & 0 & 0 \\
0& 0 & i & 1 \\
0& 0 & 0 & -1 \\
1& -i & 0 & 0 \\
\end{pmatrix}
\end{align}Theorem 1
\begin{align}
Let \space U \in SO(4)\\
MUM^*=A\otimes B \in SU(2)\otimes SU(2), \\
where A,B \in SU(2)\\
\end{align}Theorem 3
Every two-qubit quantum gate in SO(4) can be realized by a circuit consisting of 12 elementary one-qubit gates and 2 CNOT gates.
Theorem 4
It is known that every U \in U(4) can be written as
\begin{align}
U=(A_1 \otimes A_2) \cdot \bold{N}(\alpha, \beta, \gamma) \cdot (A_3 \otimes A_4)\\
where \space A_j \space \in \bold{U}(2) \\
and \space \bold{N}(\alpha, \beta, \gamma) = [exp(i(\alpha\sigma_x\otimes\sigma_x+\beta\sigma_y\otimes\sigma_y+\gamma\sigma_z\otimes\sigma_z))]\\
\alpha, \beta, \gamma \in \R
\end{align}Note that if U ∈ SU(4), then we can choose all operations Aj in (1) from SU(2)
Theorem 5
Every two-qubit quantum gate in U(4) can be realized, up to a global phase, by a circuit consisting of 3 CNOT gates and 15 elementary one-qubit gates from the family {R_x, R_z}.
They persist that…
They prove that this construction is optimal, in the sense that there is no smaller circuit, using the same
family of gates, that achieves this operation. In addition, we show that if the unitary matrix corresponding to our desired gate is purely real, it can be achieved using at most 2 CNOT gates and 12 one-qubit gates.
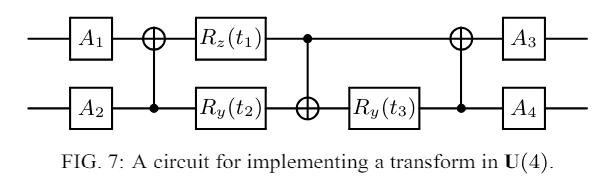
The key to the implementation here is the minimum number of CNOT gates required.
They mentioned that there are 3 gates are needed.