About
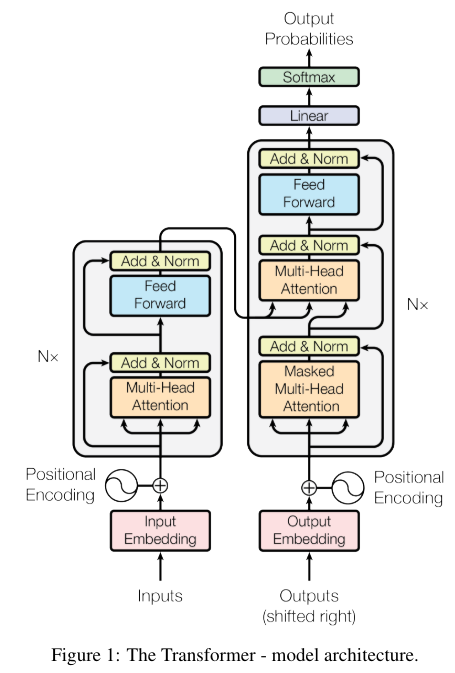
The Transformer model, incorporating an attention mechanism, has reached a peak of prosperity. It is widely used not only in natural language processing tasks but also in image recognition tasks, making it extremely important to be familiar with. It is a very convenient and useful technology; however, its structure is significantly different from previous convolutional and recurrent models, so I will present a note for easy recall at a glance.
Queue-Key-Value
The essential elements of the attention mechanism involve encoding using the query, key, and value. The original paper describes it using the following mathematical formula.
Attention(Q, K, V ) = softmax(\frac{QK^T}{\sqrt{d_k}})VFirst, I will explain the matrix calculation between the query and the key using a diagram.
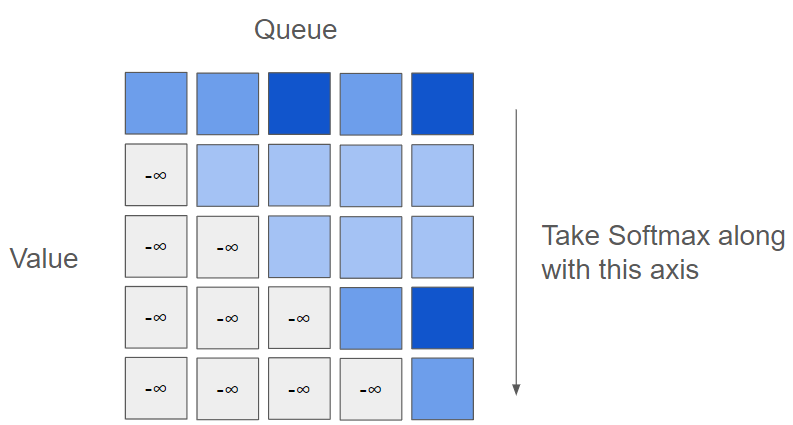
Both the query and the key are generated from encoded features (embeddings) that have undergone a linear transformation. The product of the query and key matrices is taken, and then a Softmax is applied along the key direction. Since this computation is equivalent to a dot product operation, the mechanism is designed to identify the relationships between features.
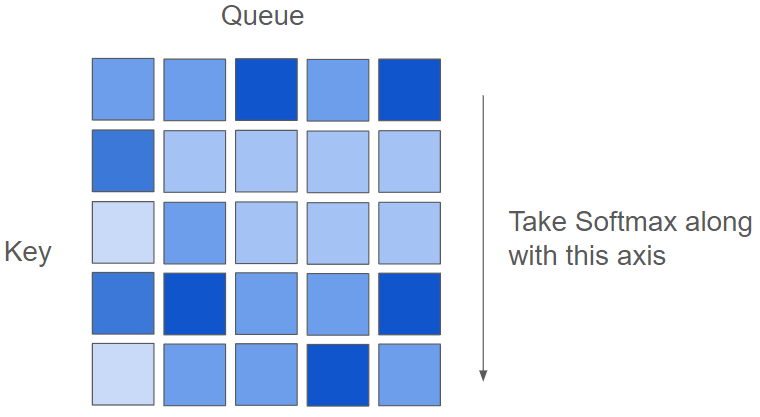
The GPT like a model used in language model, attention mask is used in order not to pay attention the sentence after the keywords. By setting the dot product values for a particular word to negative infinity, the attention values can be made zero when the Softmax is applied. This effectively allows certain words to be ignored in the attention mechanism.

\begin{align}
W_Q=\begin{pmatrix}
q_{11} & q_{12} & \cdots & q_{1n} \\
q_{21} & q_{22} & \cdots & q_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
q_{m1} & q_{m2} & \cdots & q_{mn}\\
\end{pmatrix}\\
W_K=\begin{pmatrix}
k_{11} & k_{12} & \cdots & k_{1n} \\
k_{21} & k_{22} & \cdots & k_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
k_{m1} & k_{m2} & \cdots & k_{mn}\\
\end{pmatrix}\\
m=128, n=12288
\end{align}The second step is to get value, one of the method is matrix multiplication so called low rank transformation.
\begin{align}
V=\begin{pmatrix}
v_{11} & v_{12} & \cdots & v_{1n} \\
v_{21} & v_{22} & \cdots & v_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
v_{m1} & v_{m2} & \cdots & v_{mn}\\
\end{pmatrix}\\
W_V=V V^T\\
m=12288, n=128
\end{align}What we obtain is the amount of change from the original meaning of the word’s embedding. Interpreted from the calculation process, this represents the extent to which the embedding has changed when considering the context. So in the original paper, the vector which is obtained from Multi-Head Attention, is simply added and normalized on input vector.
Reference
Attention is all you need: https://arxiv.org/pdf/1706.03762