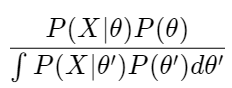About
In BoTorch, there are 2 fitting functions are prepared, fit_gpytorch_mll / fit_fully_bayesian_model_nuts(https://botorch.org/api/fit.html). And there are some loss functions are prepare to fit the models(https://docs.gpytorch.ai/en/stable/marginal_log_likelihoods.html). We will see the overview In this article.
fit_gpytorch_mll
It optimizes GPs by using marginal-log-likelihood(MLL). As we can see my article(https://eye.kohei-kevin.com/2024/03/09/1729/), GPs are described as following.
p(y | X, \theta) = \mathcal{N}(y | 0, K(X, \theta) + \sigma^2 I)If we take MLL over the probability, it is simply written as
\log p(y | X, \theta) = -\frac{1}{2} y^\top [K(X, \theta) + \sigma^2 I]^{-1} y - \frac{1}{2} \log \det(K(X, \theta) + \sigma^2 I) - \frac{n}{2} \log 2\piBasically, what the BoTorch optimize is this MLL over parameters. But actually, there are manly LogLikelihoods are implemented. These MLL be categorized into 2 classes, the one for Exact GP and for ApproximateGP. The first one is used when exact definition of MLL is demanded. The second one is used when exact inference is intractable (either when the likelihood is non-Gaussian likelihood, or when there is too much data for an ExactGP model).
- Exact GP
- ExactMarginalLogLikelihood
- LeaveOneOutPseudoLikelihood
- For ApproximateGP
- VariationalELBO
- PredictiveLogLikelihood
- GammaRobustVariationalELBO
- DeepApproximateMLL
For ApproximateGP, the idea of ELBO is basically used. It means that the model has latent variables.
fit_fully_bayesian_model_nuts
It fit a fully Bayesian model using the No-U-Turn-Sampler. In fit_gpytorch_mll manner, it basically fits a model thru MLL as loss function whereas fit_fully_bayesian_model_nuts, the MLL s not passed to the function(just a model SaasFullyBayesianSingleTaskGP | SaasFullyBayesianMultiTaskGP). The GP models are fully Bayesian GP model with the SAAS prior. And the No-U-Turn Sampler is an extension of the Hamiltonian Monte Carlo (HMC) algorithm. It means that it takes time to converge to the optima, it is bayesian estimaision. I would like to search in detail in the future.