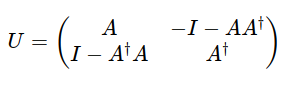Image
The image \text{Im}(A) of a matrix A describes what vectors are generated when the matrix A acts on a set of vectors. The set is defined as follows:
\text{Im}(A) = \{ A \mathbf{x} \mid \mathbf{x} \in \mathbb{R}^n \}It means that the dim of Im(A) never gets changed from original dim of A.
\dim(\text{Im}(A))=\text{rank}(A)Kernel
That is, it represents the set of all vectors \mathbf{x} that, when multiplied by the matrix A , result in a zero vector. This set is a vector space, and shows how they are mapped to zero under a linear transformation by the matrix A .
\text{Ker}(A) = \{ \mathbf{x} \in \mathbb{R}^n \mid A \mathbf{x} = \mathbf{0} \}Nullity
Nullity refers to the kernel dimension of a matrix A , i.e., the number of linearly independent vectors in \text{Ker}(A).
\text{nullity}(A) = \dim(\text{Ker}(A))So, sum of rank \text{rank}(A) + \text{nullity}(A) equals n.
\text{rank}(A) + \text{nullity}(A) = n