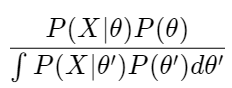About
There are some cases to compute determinants of covariance matrix such as marginal log likelihood in multi variate Gaussian distribution. I summarize how to briefly.
Get Determinant thru Cholesky decomposition
The Cholesky decomposition can be used to efficiently calculate the determinant of a matrix. The Cholesky decomposition is an efficient method for dealing with positive definite symmetric matrices. In this decomposition, the matrix is decomposed as follows:
A=LL^T
Where L is a lower triangular matrix. Using the Cholesky decomposition, the determinant can be easily calculated as follows:
det(A) = det(L) det(L^T)
Calculating determinants using Cholesky decomposition
If matrix is a positive definite symmetric matrix and can be expressed as by Cholesky decomposition, the determinant is calculated as follows:
det(L)=det(L^T)
However, is the transpose of , and the following holds due to the nature of matrix determinants:
Therefore,
det (A) = det(L)^2
Furthermore, since the determinant of a triangular matrix is given by the product of its diagonal elements, using the diagonal element of , it can be expressed as follows:
det( A) = ( prod {l_{ii}} )
