DeepSDF

https://arxiv.org/abs/1901.05103

About

There are so many methods suggested to represent 3D shapes such as mesh, point cloud or volume. But these method is not so able to generate clean 3D shape. To address the issue, DeepSDF is suggested. It seems a bit old paper, but this idea is important even nowadays.

SDF

The Signed Distance Function (SDF) is a mathematical function used to describe the geometry of a shape in space. It assigns a scalar value to every point in the space based on the following rules:

\text{SDF}(\mathbf{p}) = 
\begin{cases} 
\text{Distance}(\mathbf{p}, \partial\Omega) & \text{if } \mathbf{p} \text{ is outside the shape,} \\
-\text{Distance}(\mathbf{p}, \partial\Omega) & \text{if } \mathbf{p} \text{ is inside the shape,}\\
\end{cases}\\
\text{SDF}: \mathbb{R}^3 \to \mathbb{R}, \quad \text{where } \mathbf{p} \in \mathbb{R}^3

Where:

• \mathbf{p} \in \mathbb{R}^3 )represents a point in three-dimensional space.
• \partial\Omega represents the boundary of the shape in \mathbb{R}^3 .
• \text{Distance}(\mathbf{p}, \partial\Omega) is the shortest Euclidean distance from \mathbf{p} to the surface \partial\Omega .

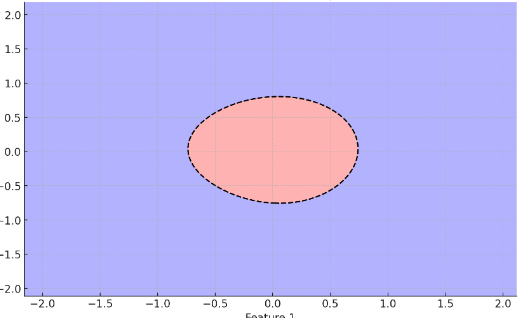
Suppose we have an object in a space above (red area). The SDF takes negative values inside red area, and takes positive value outside (blue), and takes 0 on the boundary.

In DeepSDF, the function is going to export SDF values via Neural Network.

DeepSDF Optimization

By utilizing SDFs (Signed Distance Functions) in Deep Learning, various benefits can be achieved. For example, it becomes possible to obtain extremely smooth curves or handle complex shapes. But how can we optimize the networks?

The function that they optimized is here.

\begin{align}
\arg\min_{\theta, \{z_i\}_{i=1}^N} \sum_{i=1}^N \left( \sum_{j=1}^K L\big(f_\theta(z_i, x_j), s_j\big) + \frac{1}{\sigma^2} \|z_i\|_2^2 \right)\\
L(f_\theta(x), s) = \left| \text{clamp}(f_\theta(x), \delta) - \text{clamp}(s, \delta) \right|\\
  \text{clamp}(y, \delta) =
  \begin{cases} 
  \delta & \text{if } y > \delta, \\
  -\delta & \text{if } y < -\delta, \\
  y & \text{otherwise.}
  \end{cases}
\end{align}

where

• z_i is a latent variables
• f_\theta is NN which takes 3D points and latent code as input, and export SDF as output
• N, K is the number of objects and points respectively

How to encode shape information?

I felt that the interesting part of DeepSDF is encoding parts. The function that encodes shape is NOT auto-encoder. The thing is that they do not use encoder, they just use decoder in their model which is so called Auto-Decoder. It means that latent variables is randomly assigned initially, and then is going to be trained.

Since the model does not have encoder, we need to embed shape information into latent space somehow? How do we do that? Actually, we can do MAP (maximum a posterior) estimation by minimizing below function.

\hat{z} = \arg \min_{z} \sum_{(x_j, s_j) \in \mathcal{X}} L(f_\theta(z, x_j), s_j) + \frac{1}{\sigma^2} \|z\|_2^2.

By optimizing this function using data itself, we can get embedded latent variables from shape information. But what is the advantage of using it?

In some problem settings, auto encoders are not able to embed shape information that has only a part of whole shape into suitable latent space since information is lacking. It means that the lacked information is handled as it is. Because of this point, we cannot use auto encoder based methods for reconstruction problems like recovering 3D shape from depth camera. This characteristic of algorithm is good for shape completion or shape restoration problems.

And also, they claimed that the the stochastic nature of the VAE optimization did not lead to good training results.