Python library for topology optimization built on top of Scikit Libraries
About
I implemented topology optimization based on Scikit and Scikit-FEM.
While there are many open-source projects focusing on topology optimization, not all of them are practical. Many are limited to 2D cases or can only handle grid-based geometries, which restricts their applicability. To overcome these limitations, I developed a mesh-based topology optimization framework using Scikit-FEM, enabling the handling of more complex geometries. Additionally, by integrating PyAMG, the framework also supports multigrid solvers.
https://github.com/kevin-tofu/scikit-topt
Please take a look at the example below.
Examples
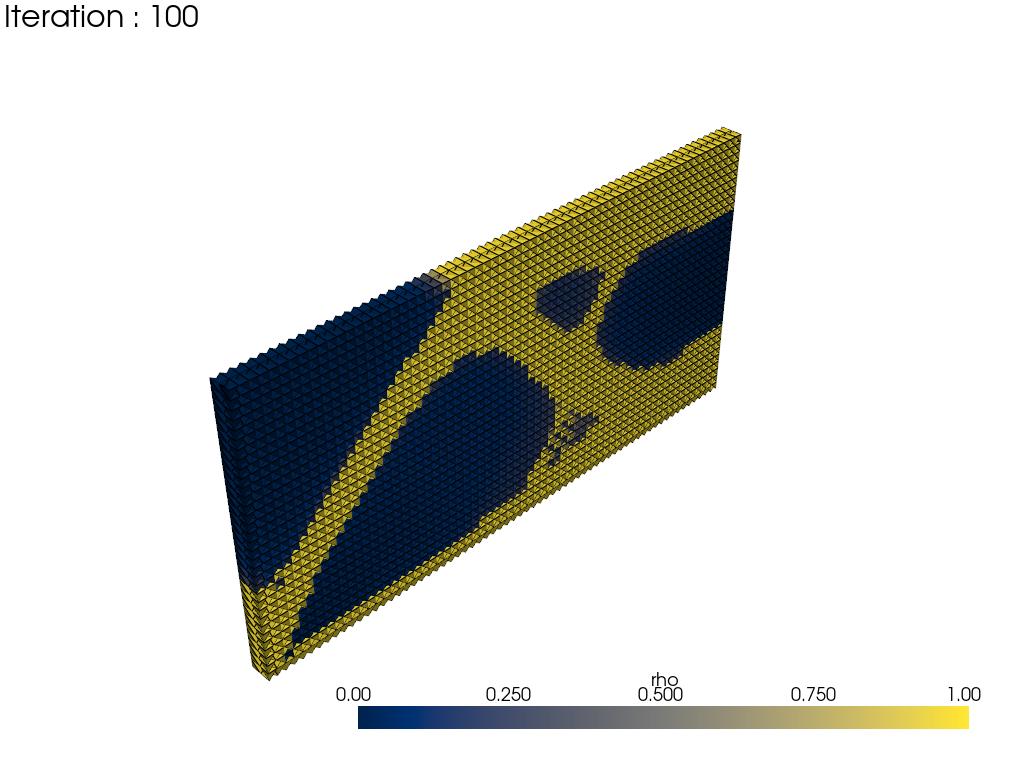

In the case of Multiple Load Condition
This library is able to take multiple load condition into account. For example, suppose if load F is imposed opposite direction on the corner of the object below, and Dirichlet BCs are set on the top surface on the object.

The results are shown in below, the left one is obtained when volume constraint is 50%, and the right one is when volume constraint is 30%.
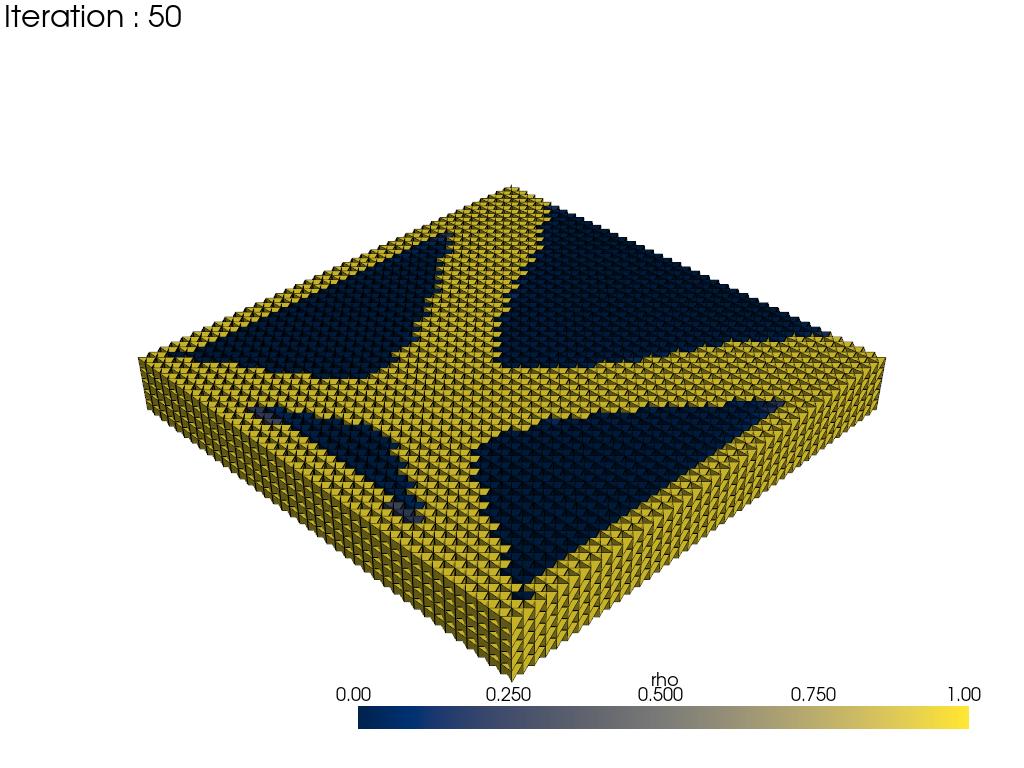
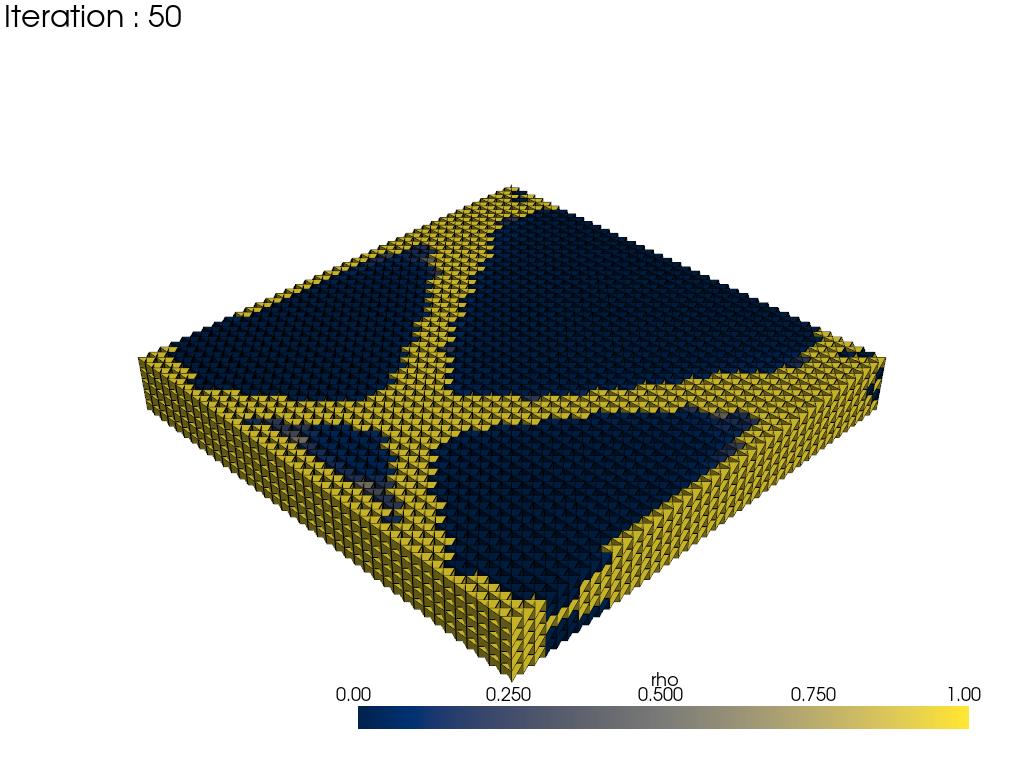
Techniques
Optimization – OC Method
Please take a look at article here.
Optimization – Lagrangian Method
Unlike the OC method, which is tailored mainly for problems like compliance minimization with simple volume constraints, the Lagrange method can systematically handle multiple and complex constraints, such as stress, displacement bounds, or manufacturing limitations. This makes it more suitable for multi-objective or real-world optimization problems where flexibility is required. However, this generality comes to expensive computational cost.
SIMP (Solid Isotropic Material with Penalization)
SIMP is the most commonly used interpolation scheme:
E(ρ) = ρ^p * E₀
RAMP (Rational Approximation of Material Properties)
RAMP is another interpolation scheme used to reduce numerical instabilities like checkerboarding:
E(ρ) = E₀ * ρ / (1 + q * (1 - ρ))
Heaviside Projection
Heaviside projection is used to sharpen the boundaries between solid and void regions after filtering:
ρ̃ = (tanh(β * η) + tanh(β * (ρ - η))) / (tanh(β * η) + tanh(β * (1 - η)))
Helmholtz Filter
The Helmholtz filter smooths the density field to prevent checkerboard patterns and enforce a minimum feature size.
It solves the PDE:
(-r² ∇² + 1) ρ̃ = ρ
Continuation
Continuation is a strategy used in topology optimization to gradually change certain parameters during the optimization process, rather than keeping them fixed. The purpose is to improve convergence, avoid poor local minima, and help the algorithm find good structures for human.
In SIMP-based methods, continuation is commonly applied to parameters like the penalization power (p), projection sharpness (β in Heaviside projection), or volume fraction. For example, starting with a small penalization value and slowly increasing it during the optimization can prevent premature convergence to binary designs and allow finer control over the material distribution. Similarly, increasing the projection parameter helps sharpen the intermediate densities into clearer black-and-white structures.
Visualization
I have implemented functionality to monitor the evolution of the density distribution and parameters, allowing users to verify whether the algorithm is operating as intended. By observing these transitions, the system supports fine-tuning of the parameters to achieve better optimization results.
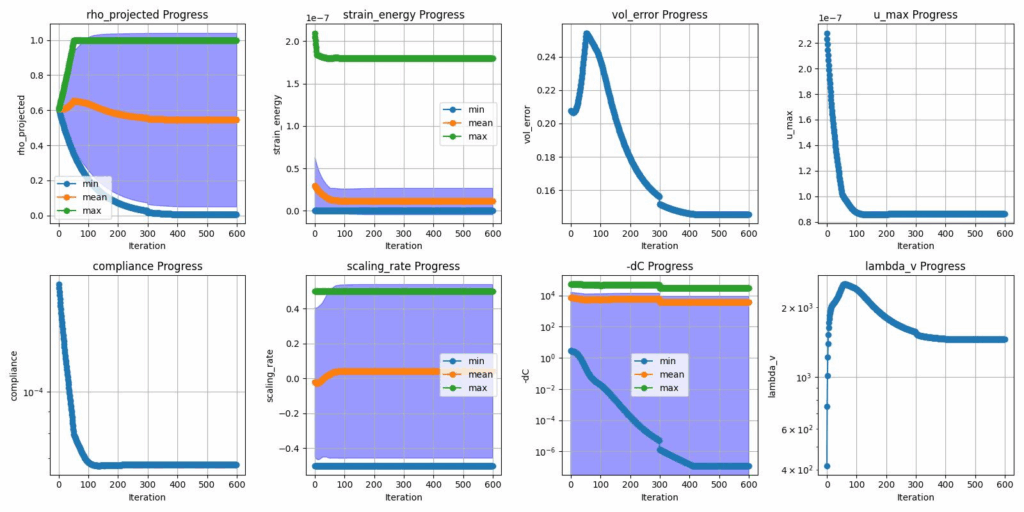
Reference
https://github.com/kevin-tofu/scikit-topt