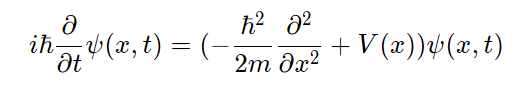
What is Lagrangian and Hamiltonian?
- The Lagrangian is a function used to derive how a system moves (i.e., the equations of motion).
- The Hamiltonian is a function that describes the energy state of the system, specifically conserved quantities.
These are able to handle a system in a unified way even in complex coordinate systems.
Differentials in Hamiltonian
What does it mean?
Well, You don’t have to worry about coordinate systems when writing the equations of motion using the Hamiltonian. Hamilton’s canonical equation is
\dot{q}_i = \frac{\partial H}{\partial p_i}, \quad \dot{p}_i = -\frac{\partial H}{\partial q_i}This format can be used as is regardless of the coordinate system used.
For example, whether you use Cartesian or polar coordinates, you can obtain the same form of equation of motion by properly defining the generalized coordinates q_i.
Euler–Lagrange equation (of motion) is as follows:
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right) - \frac{\partial L}{\partial q_i} = 0How Lagrangian is related with Hamiltonian?
The Hamiltonian extracts an energy-based perspective from the Lagrangian. As you can see, The Hamiltonian is defined from the Lagrangian.
H(q, p) = \sum_i p_i \dot{q}_i - L(q, \dot{q})where p_i = \frac{\partial L}{\partial \dot{q}_i} is generalized momentum, \dot{q}_i is generalized velocity, and L is Lagrangian.
The Lagrangian
L = T - V = \frac{1}{2} m \dot{x}^2 - \frac{1}{2} k x^2 \\ Generalized Momentum
p = \frac{\partial L}{\partial \dot{x}} = m \dot{x}
\Rightarrow \dot{x} = \frac{p}{m}The definition of Hamiltonian
H = p \dot{x} - L = \frac{p^2}{m} - \left( \frac{1}{2} m \dot{x}^2 - \frac{1}{2} k x^2 \right)This is exactly T+V, the total energy.
| Aspect | Lagrangian L=T−V | Hamiltonian H=T + V |
|---|---|---|
| Meaning | Describes how the system moves. focus on the trajectory of motion itself | Describes what energy the system has, and describe the structure of time evolution (dynamical system structure) |
| Purpose | Deriving equations of motion | Describing energy conservation, evolution, and quantization |
| Variables | q, \dot{q}(position and velocity) | q,p(position and momentum) |
| Mathematical Link | H=pq˙−LH = p \dot{q} - L | Derived from the Lagrangian |