Benchmark : scikit-fem vs mfem

About

Scikit-fem is an excellent library. Since it is written in pure Python, it is highly stable and makes it easy to see exactly what kind of computations are being performed. However, its computation speed is generally slower compared to C++-based libraries. Therefore, I decided to compare it with another library called MFEM. MFEM also provides a Python API, which makes it relatively easy to solve the same problem for comparison.

Benchmark

Generate mesh as toy problem with Gmesh

The code below generates points in which size is (3, 10350). It is tensile problem, what we are going to do is to set dirichlet bc on the bottom, and pull the surface on the top.

import gmsh

gmsh.initialize()
gmsh.model.add("tension_bar")

L, W, H = 1.0, 0.1, 0.1
lc = 0.01

gmsh.model.occ.addBox(0, 0, 0, L, W, H)
gmsh.model.occ.synchronize()

# --- サイズ制御を追加 ---
gmsh.option.setNumber("Mesh.CharacteristicLengthMin", lc)
gmsh.option.setNumber("Mesh.CharacteristicLengthMax", lc)

# --- 物理グループ設定 ---
left = gmsh.model.occ.getEntitiesInBoundingBox(0, 0, 0, 0, W, H, 2)
gmsh.model.addPhysicalGroup(2, [s[1] for s in left], tag=1)
gmsh.model.setPhysicalName(2, 1, "fixed")

right = gmsh.model.occ.getEntitiesInBoundingBox(L, 0, 0, L, W, H, 2)
gmsh.model.addPhysicalGroup(2, [s[1] for s in right], tag=2)
gmsh.model.setPhysicalName(2, 2, "load")

vol = gmsh.model.occ.getEntities(dim=3)
gmsh.model.addPhysicalGroup(3, [vol[0][1]], tag=10)
gmsh.model.setPhysicalName(3, 10, "bar")

gmsh.option.setNumber("Mesh.MshFileVersion", 2.2)
gmsh.model.mesh.generate(3)
gmsh.write("tension_bar.msh")

gmsh.finalize()
print("✅ Saved: tension_bar.msh (Gmsh 2.2 format)")

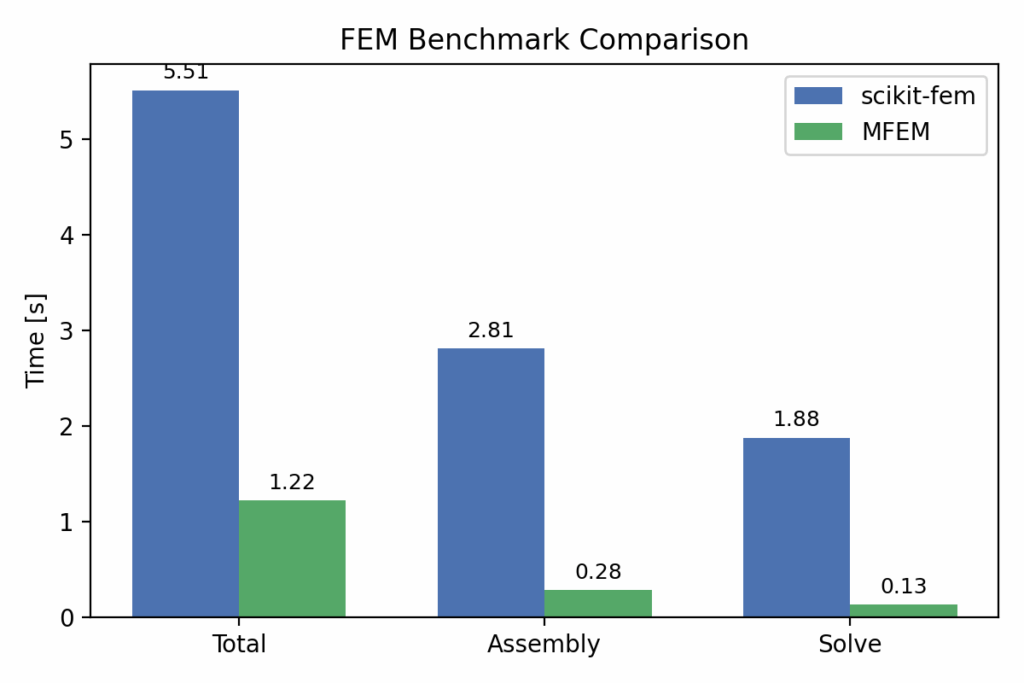
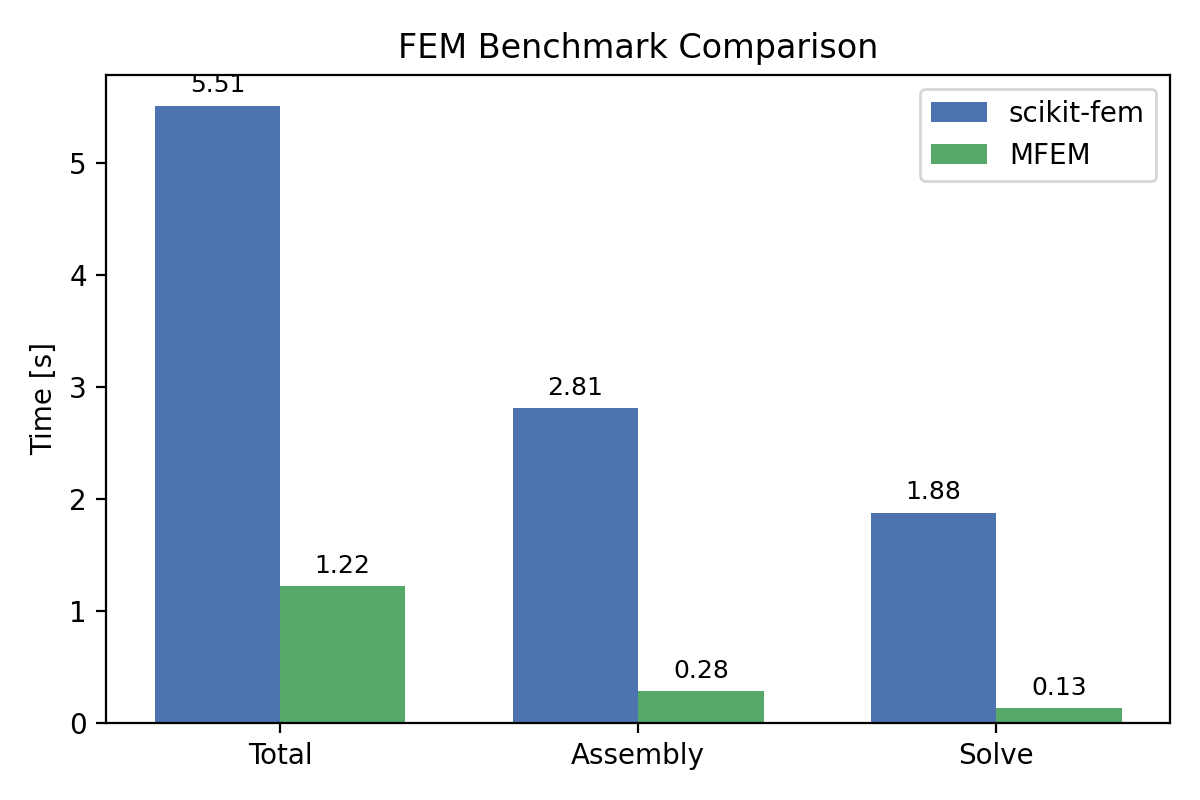
Comparison ( Assembling, Solve, and Total)

import time
import numpy as np
import skfem as sk
# import mfem.par as mfem
import mfem.ser as mfem



def run_skfem(mesh_file: str):
    from skfem.models.elasticity import lame_parameters
    from skfem.models.elasticity import linear_elasticity
    from skfem.helpers import dot

    E, nu = 210e9, 0.3
    lam, mu = lame_parameters(E, nu)

    t0_total = time.perf_counter()
    mesh = sk.MeshTet.load(mesh_file)
    print(f"mesh.p {mesh.p.shape}")
    basis = sk.Basis(mesh, sk.ElementVector(sk.ElementTetP1()))

    # @sk.BilinearForm
    # def elasticity(u, v, w):
    #     eps_u, eps_v = sk.sym_grad(u), sk.sym_grad(v)
    #     return lam * sk.trace(eps_u) * sk.trace(eps_v) + 2 * mu * sk.ddot(eps_u, eps_v)

    @sk.LinearForm
    def traction(v, w):
        # return sk.dot(np.array([1e6, 0, 0]), v)
        return 10e3 * dot(w.n, v)


    left = mesh.facets_satisfying(lambda x: np.isclose(x[0], 0))
    right = mesh.facets_satisfying(lambda x: np.isclose(x[0], 1.0))
    fixed = basis.get_dofs(facets=left).all()
    fbasis = sk.FacetBasis(
        mesh, sk.ElementVector(sk.ElementTetP1()), facets=right
    )

    # アセンブリ
    t0 = time.perf_counter()
    # K = sk.asm(elasticity, basis)
    K = linear_elasticity(lam, mu).assemble(basis)
    F = sk.asm(traction, fbasis)
    t_asm = time.perf_counter() - t0

    # Dirichlet条件 + 解く
    K, F = sk.enforce(K, F, D=fixed)
    t1 = time.perf_counter()
    u = sk.solve(K, F)
    t_solve = time.perf_counter() - t1

    t_total = time.perf_counter() - t0_total

    print(f"[scikit-fem] Total: {t_total:.3f}s | Assembly: {t_asm:.3f}s | Solve: {t_solve:.3f}s | max|u|={np.abs(u).max():.3e}")
    return mesh.p.T, u.reshape(-1, 3), [t_total, t_asm, t_solve]


def run_mfem(mesh_file: str):
    """MFEMによる構造解析（全処理時間計測）"""
    E, nu = 210e9, 0.3
    mu = E / (2 * (1 + nu))
    lam = E * nu / ((1 + nu) * (1 - 2 * nu))

    t0_total = time.perf_counter()
    mesh = mfem.Mesh(mesh_file, 1, 1, True)
    dim = mesh.Dimension()
    fec = mfem.H1_FECollection(1, dim)
    fespace = mfem.FiniteElementSpace(mesh, fec, dim)

    # 拘束面 (x=0)
    ess_bdr = mfem.intArray(mesh.bdr_attributes.Max())
    ess_bdr.Assign(0)

    for be in range(mesh.GetNBE()):
        attr = mesh.GetBdrAttribute(be)
        if attr <= 0:
            continue
        vertex_ids = mesh.GetBdrElementVertices(be)

        # ✅ 座標を安全に取得
        pts = np.array([np.array(mesh.GetVertexArray(int(idx))) for idx in vertex_ids])
        center = np.mean(pts, axis=0)

        if np.isclose(center[0], 0.0):
            ess_bdr[attr - 1] = 1


    # 弾性積分子
    a = mfem.BilinearForm(fespace)
    a.AddDomainIntegrator(mfem.ElasticityIntegrator(
        mfem.ConstantCoefficient(lam),
        mfem.ConstantCoefficient(mu)))

    # 面荷重 (x=L)
    traction = mfem.VectorConstantCoefficient(mfem.Vector([1e6, 0, 0]))
    L = mfem.LinearForm(fespace)
    L.AddBoundaryIntegrator(mfem.VectorBoundaryLFIntegrator(traction))

    # アセンブリ
    t0 = time.perf_counter()
    a.Assemble()
    L.Assemble()
    t_asm = time.perf_counter() - t0

    # 系を形成して解く
    x = mfem.GridFunction(fespace)
    a.EliminateEssentialBC(ess_bdr, x, L)

    # ✅ SparseMatrix版（シリアルMFEM対応）
    A = mfem.SparseMatrix()
    X = mfem.Vector()
    B = mfem.Vector()
    a.FormLinearSystem(ess_bdr, x, L, A, X, B)

    solver = mfem.CGSolver()
    solver.SetOperator(A)
    solver.SetRelTol(1e-8)
    solver.SetAbsTol(0.0)
    solver.SetMaxIter(1000)
    solver.SetPrintLevel(0)

    t1 = time.perf_counter()
    solver.Mult(B, X)
    t_solve = time.perf_counter() - t1

    t_total = time.perf_counter() - t0_total

    # 変位をfespace上に戻す
    a.RecoverFEMSolution(X, L, x)

    # 座標と変位をNumPy配列で取得
    coords = np.array([mesh.GetVertexArray(i) for i in range(mesh.GetNV())])
    
    # ✅ GetDataArray() で内部データを取得し、節点ごとに3成分にreshape
    disp = np.array(x.GetDataArray()).reshape(-1, 3)

    print(f"[MFEM]       Total: {t_total:.3f}s | Assembly: {t_asm:.3f}s | Solve: {t_solve:.3f}s | ndofs={fespace.GetNDofs()}")
    return coords, disp, [t_total, t_asm, t_solve]


def visualize(
    skfem_times, mfem_times,
    dst_path: str = "benchmark_comparison.png"
):
    import matplotlib.pyplot as plt
    import numpy as np

    # データ（あなたの測定結果）
    labels = ["Total", "Assembly", "Solve"]
    
    x = np.arange(len(labels))  # X軸位置
    width = 0.35                # 棒の幅

    fig, ax = plt.subplots(figsize=(6, 4))
    rects1 = ax.bar(x - width/2, skfem_times, width, label='scikit-fem', color='#4C72B0')
    rects2 = ax.bar(x + width/2, mfem_times, width, label='MFEM', color='#55A868')

    # 軸ラベル・タイトル
    ax.set_ylabel('Time [s]')
    ax.set_title('FEM Benchmark Comparison')
    ax.set_xticks(x)
    ax.set_xticklabels(labels)
    ax.legend()

    # 各棒に値を表示
    def autolabel(rects):
        for rect in rects:
            height = rect.get_height()
            ax.annotate(f'{height:.2f}',
                        xy=(rect.get_x() + rect.get_width() / 2, height),
                        xytext=(0, 3),
                        textcoords="offset points",
                        ha='center', va='bottom', fontsize=9)

    autolabel(rects1)
    autolabel(rects2)

    fig.tight_layout()
    plt.savefig(dst_path, dpi=200)
    # plt.show()

    print("✅ Saved: benchmark_comparison.png")


def compare_displacements(coords1, u1, coords2, u2, tol=1e-8):
    # 両メッシュが一致する前提
    assert np.allclose(coords1, coords2, atol=tol)

    diff = u1 - u2
    abs_err = np.linalg.norm(diff, axis=1)
    l2_err = np.linalg.norm(abs_err)
    rel_err = l2_err / np.linalg.norm(np.linalg.norm(u1, axis=1))
    max_err = np.max(abs_err)

    print(f"‣ L2 error = {l2_err:.3e}")
    print(f"‣ Relative L2 error = {rel_err:.3e}")
    print(f"‣ Max abs error = {max_err:.3e}")


if __name__ == "__main__":
    msh = "tension_bar.msh"  # Gmshで生成済みメッシュ

    skfem_coords, skfem_disp, skfem_times = run_skfem(msh)
    mfem_coords, mfem_disp, mfem_times = run_mfem(msh)
    tT_s, tA_s, tS_s = skfem_times
    tT_m, tA_m, tS_m = mfem_times

    compare_displacements(skfem_coords, skfem_disp, mfem_coords, mfem_disp)

    print("\n=== Benchmark Summary ===")
    print(f"scikit-fem: Total {tT_s:.3f}s | Assembly {tA_s:.3f}s | Solve {tS_s:.3f}s")
    print(f"MFEM:       Total {tT_m:.3f}s | Assembly {tA_m:.3f}s | Solve {tS_m:.3f}s")

    visualize(
        skfem_times, mfem_times,
    )

Result