Introduction
As discussed in the previous article, in the density-based SIMP method it is not possible to impose a strict Robin boundary condition on unknown boundaries.
As a result, the objective function cannot be updated according to the newly formed boundaries.
To address this issue, a virtual Robin boundary condition was applied to the generated boundaries to observe how the shape evolves.
Virtual Robin Condition
The original Robin boundary condition is expressed as follows:
\mathbf{q} \cdot \mathbf{n} = h (T - T_{\text{env}}) \quad \text{on } \Gamma_R
\\
\int_{\Gamma_R} h T v d\Gamma = \int_{\Gamma_R} h T_{\text{env}} v d\Gamma
In topology optimization, we want to allow heat dissipation on the newly formed internal interfaces within the structure. However, since the entire analysis domain \Omega is fixed, we do not explicitly know where those interfaces are. Therefore, we approximate the effect using a volume integral weighted by the interface gradient |\nablaρ|.
\int_{\Omega} h_\text{eff}(\rho) |\nabla \rho| (T - T_{\text{env}}) v d\Omega\\
where \space h_\text{eff}(\rho)=h_0\rho(1-\rho)\\
Or \space h_{\text{eff}}(\rho) = h_0 \rho^p (1 - \rho)^qMoreover, the heat dissipation on the actual Robin boundaries should also be modified to be density-dependent.
h_{\mathrm{eff}}(\rho) = h_0 \rho^p\\
\int_{\Gamma_R} h_{\mathrm{eff}}(\rho)(T - T_{\mathrm{env}})vd\Gamma
= \int_{\Gamma_R} h_0\rho^p(T - T_{\mathrm{env}})vd\GammaResult
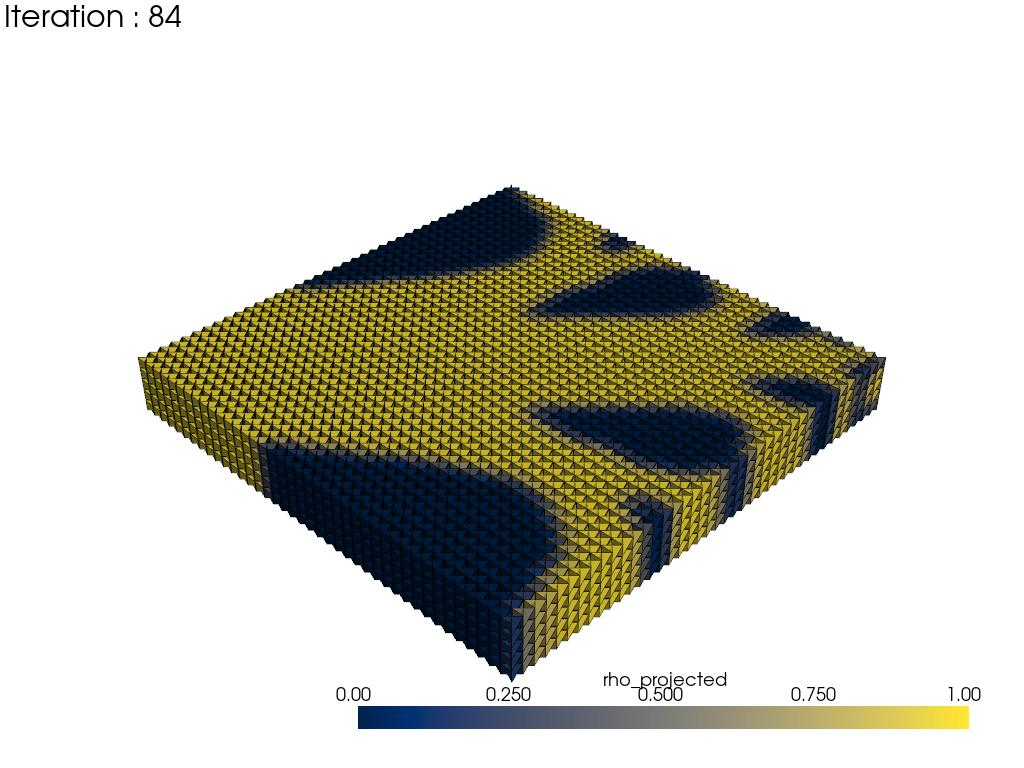
Density Distribution
There are some rooms to be improved though, so far so good.