Key Idea
MAML, Meta-SGD, and Reptile have almost the same steps for optimization. The procedures are shown in Figure 1[1]. To begin with, the support set and the query set are sampled from the dataset, and make tasks using the support set. Now we have n tasks when we have n support set. And on the inner loop, we are going to learn n tasks and then, get optimized n models from the same randomly initialized parameter. Finally, on the outer loop, the randomly initialized parameter is going to be optimized by the model parameters which are gotten from the inner loop. Figure 2. visualize how these steps are expected to work. When this framework has 3 tasks, we are going to get general direction to be converged using 3 model parameters from 3 tasks. These 3 model parameters are computed on the inner loop and then, a model parameter as a good initial point is optimized on the outer loop.

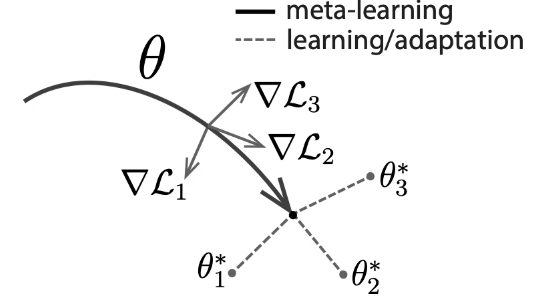
So what is the difference between these 3 types of Meta-Learning?
MAML
\begin{align}
T_i \text{\textasciitilde} p(T) \\
T = \text{\textbraceleft} T_1, T_2, T_3,,,, T_n \text{\textbraceright}\\
{\theta}_i^{'} = \theta - \alpha {\nabla}_{\theta}L_{T_i}(f_{\theta})
\end{align}\begin{align}
{\theta}^{'} = \text{\textbraceleft} {\theta}_1, {\theta}_2, {\theta}_3,,,, {\theta}_n \text{\textbraceright}\\
{\theta} = {\theta} - \beta\nabla_{\theta} \sum_{T_i \text{\textasciitilde} p(T) \\} L_{T_i}(f_{\theta_i^i})\\
\end{align} Meta-SGD
For updating θ’ on each inner loop, Meta-SGD is going to use equation (6) instead of equation (3). What is the difference? Yeah, the α looks a bit different. In Meta-SGD the α is a vector, not a scalar. The vector α is randomly initialized and each weight in the vector is applied for each gradient. That means, therefore we do not know good values of α, we have to optimize α as well. The procedure of updating α is shown in equation (8). This update is going to be done in the outer loop.
\begin{align}
{\theta}_i^{'} = \theta - \mathring{\alpha} \circ {\nabla}_{\theta}L_{T_i}(f_{\theta})\\
\end{align}The procedure of updating alpha is almost as same as the procedure of updating θ except the derivative is computed with respect to α.
\begin{align}
{\theta} = {\theta} - \beta\nabla_{\theta} \sum_{T_i \text{\textasciitilde} p(T) \\} L_{T_i}(f_{\theta_i^i})\\
\mathring{\alpha} = \mathring{\alpha} - \beta\nabla_{\mathring{\alpha}} \sum_{T_i \text{\textasciitilde} p(T) \\} L_{T_i}(f_{\theta_i^i})\\
\end{align}Meta-SGD can be applied to any supervised learning problem setting.
Reptile
The 2 methods above on the outer step to update θ are just using the loss function for the tasks as it is. But in Reptile, it is a bit different. The loss function on the outer loop on Reptile is the mean least square error between parameters. It means that we are going to get a model parameter that is on the average squared distance between optimized parameters on the inner loop.
There are some good points. First, unlike MAML, it is computationally efficient. Second, it implies that the outer loop optimization is indirectly using the second-order derivative over the loss. Reptile is not computing the second order derivative itself directly nor expanding the computational graph, nevertheless, it has absolutely a good characteristic of optimization.
\begin{align}
\theta = d(\theta)=argmin_{\theta} \sum [\frac{1}{2}D({\theta}, {\theta}^{'})]^2
\end{align}\begin{align}
\theta = {\theta} - \epsilon{\nabla}_{\theta} d(\theta)\\
\theta = {\theta} - \epsilon[{{\theta} - \theta}^{'}]\\
\end{align}Reference
[1] Chelsea Finn, Pieter Abbeel, Sergey Levine “Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks” in https://arxiv.org/abs/1703.03400
