Interesting gimmick of diffusion process for training diffusion models

What is actual diffusion process is like on the code

The diffusion model gradually abstracts data using many steps. These single abstraction processes are represented by a common function. Whereas that of VAE, it does not specify how to transform the data into abstract representation. It is learned by back-propagation.

When I had seen diffusion process at first time below, It seems that sequential process.

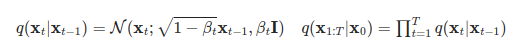
But actually, the diffusion process can be generated directly from an arbitrary initial value at a specified diffusion time.

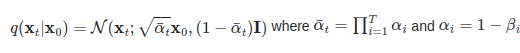
This code below shows how to generate data with gaussian noise on diffusion process using diffusers library.

import diffusers
noise_scheduler = diffusers.DDPMScheduler(num_train_timesteps=1000)
timesteps = torch.linspace(0, 999, 4).long().to(device)
noise = torch.randn_like(xb)
noisy_xb = noise_scheduler.add_noise(xb, noise, timesteps)

Training code

# Sample a random timestep for each image
# low=0, high, size
timesteps = torch.randint(
    0,
    noise_scheduler.num_train_timesteps,
    (bs,),
    device=clean_images.device
).long()
# Add noise to the clean images according to the noise magnitude at each timestep
noisy_images = noise_scheduler.add_noise(
    clean_images,
    noise,
    timesteps
)
# Get the model prediction
noise_pred = model(noisy_images, timesteps, return_dict=False)[0]
# Calculate the loss
loss = F.mse_loss(noise_pred, noise)
loss.backward(loss)

Inference code

Unlike in training function, the inverse diffusion process must be inferred step-by-step. Therefore the repeated process, This calculation is somewhat time consuming.

sample = torch.randn(batch_size, 3, 32, 32).to(device)

sample = torch.randn(1, 3, 32, 32).to(device)

for i, t in enumerate(noise_scheduler.timesteps):

    # Get model pred
    with torch.no_grad():
        residual = model(sample, t).sample

    # Update sample with step
    sample = noise_scheduler.step(residual, t, sample).prev_sample