Quantum bit
Amplitude Vector
A Quantum bit (Qbit) is represented as below.
\begin{align}
Qubit = \ket{\psi} = \alpha_1\ket{0}+\alpha_1\ket{1} \\
{\alpha_1}^2+{\alpha_2}^2=1
\end{align}The above Qbit is expressed using another form, Bloch Sphere.
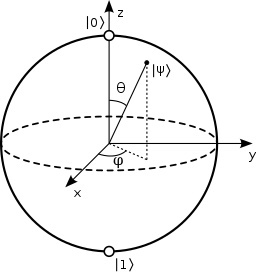
\begin{align}
\ket{\psi} = exp(i\gamma)(cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1})
\end{align}When it is separatable (not entanglement), n Qubit is described as below.
\begin{align}
\ket{\psi} = \ket{q_1}\otimes\ket{q_1}\otimes...\otimes\ket{q_n}
\end{align}But it is entanglement, N size of Qubit is described as below.
\begin{align}
\ket{\psi} = \alpha_1\ket{0000}+\alpha_2\ket{0001}\otimes...+\alpha_{2^n}\ket{1111} \\
\ket{\psi} = \displaystyle\sum_{i} \alpha_i\ket{i}
\end{align}Visualize using Bloch-Sphere
We can visualize quantum state using Bloch-Sphere.
These formula are amplitude vector, and images below is corresponding the visualized amplitude state using Bloch-Sphere.
Z_{basis-0} =(cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1})= \ket{0}\ ,\ \theta=0 \\
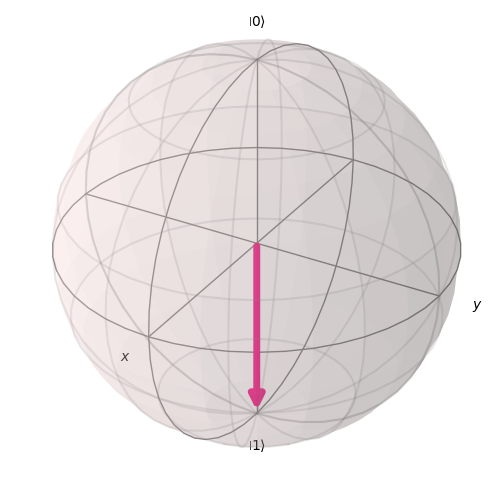
Z_{basis-1} = (cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1})= \ket{1}\ ,\ \theta=\pi \\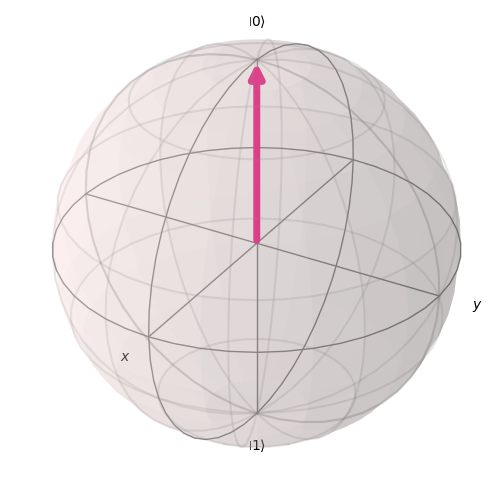
Z_{basis} = (cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1})=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})=\ket{+}\ ,\ \theta=\frac{\pi}{2}\ , \phi=0 \\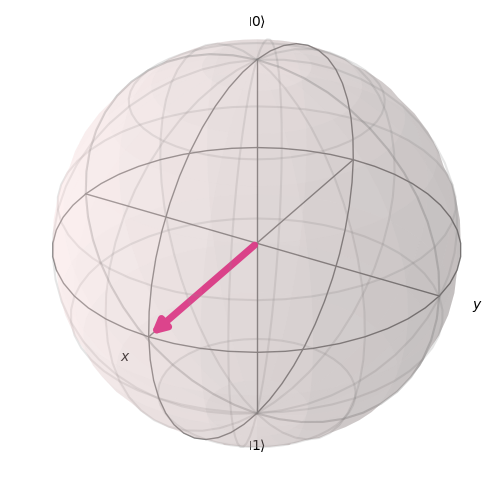
Z_{basis} = (cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1})=\frac{1}{\sqrt{2}}(\ket{0}+i\ket{1})=\ket{+i}\ ,\ \theta=\frac{\pi}{2}\ , \phi=\frac{\pi}{2} \\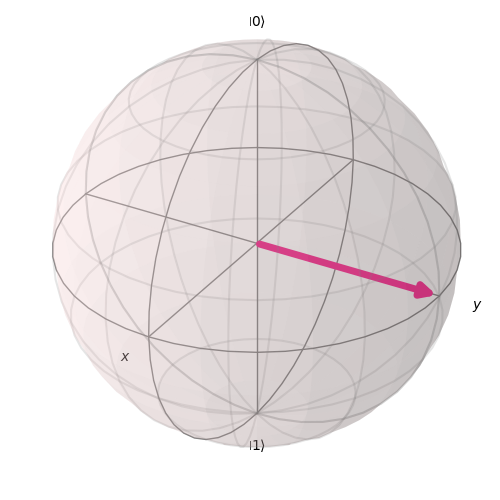
Z_{basis} = (cos{\theta\over2}\ket{0}+exp(i\phi)sin{\theta\over2}\ket{1}) ,\ \theta=\frac{\pi}{2}\ , \phi=\frac{\pi}{4} \\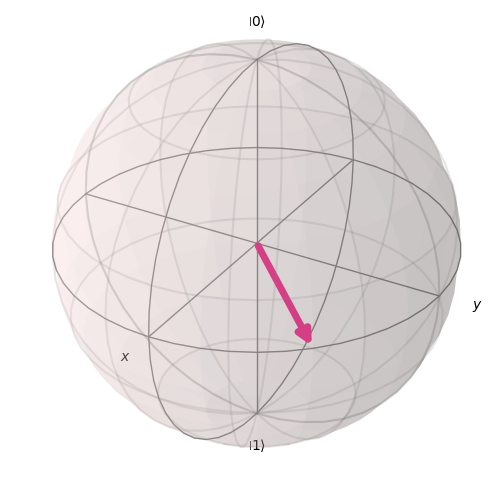
Density Matrix
When the vector is pure state,
\begin{align}
\rho_{pure} \ket{\psi}=\displaystyle\sum_{i=1}^N {\alpha_i}^*{\alpha_j}\ket{i}\bra{j} \\
\end{align}But when the vector is mixed state, since the coefficients are not separatable.
\begin{align}
\rho_{composite} \ket{\psi}=\displaystyle\sum_{i,j=1}^N {\alpha_{ij}}\ket{i}\bra{j} \\
\end{align}Quantum Gate
Just like digital circuits, which include NAND gates for classical bits, quantum gates also exist for quantum bits. Quantum gates correspond to unitary transformations applied to quantum bits.
For example, there are quantum gates equivalent to the three Pauli matrices, as well as gates such as the Hadamard gate and the CNOT gate.
Hadamard gate: A matrix used to create superposition of quantum bits.
CNOT gate: A gate that acts as a switch where, if the first quantum bit is 1, the NOT operation is performed.